MINOS/MINOS+

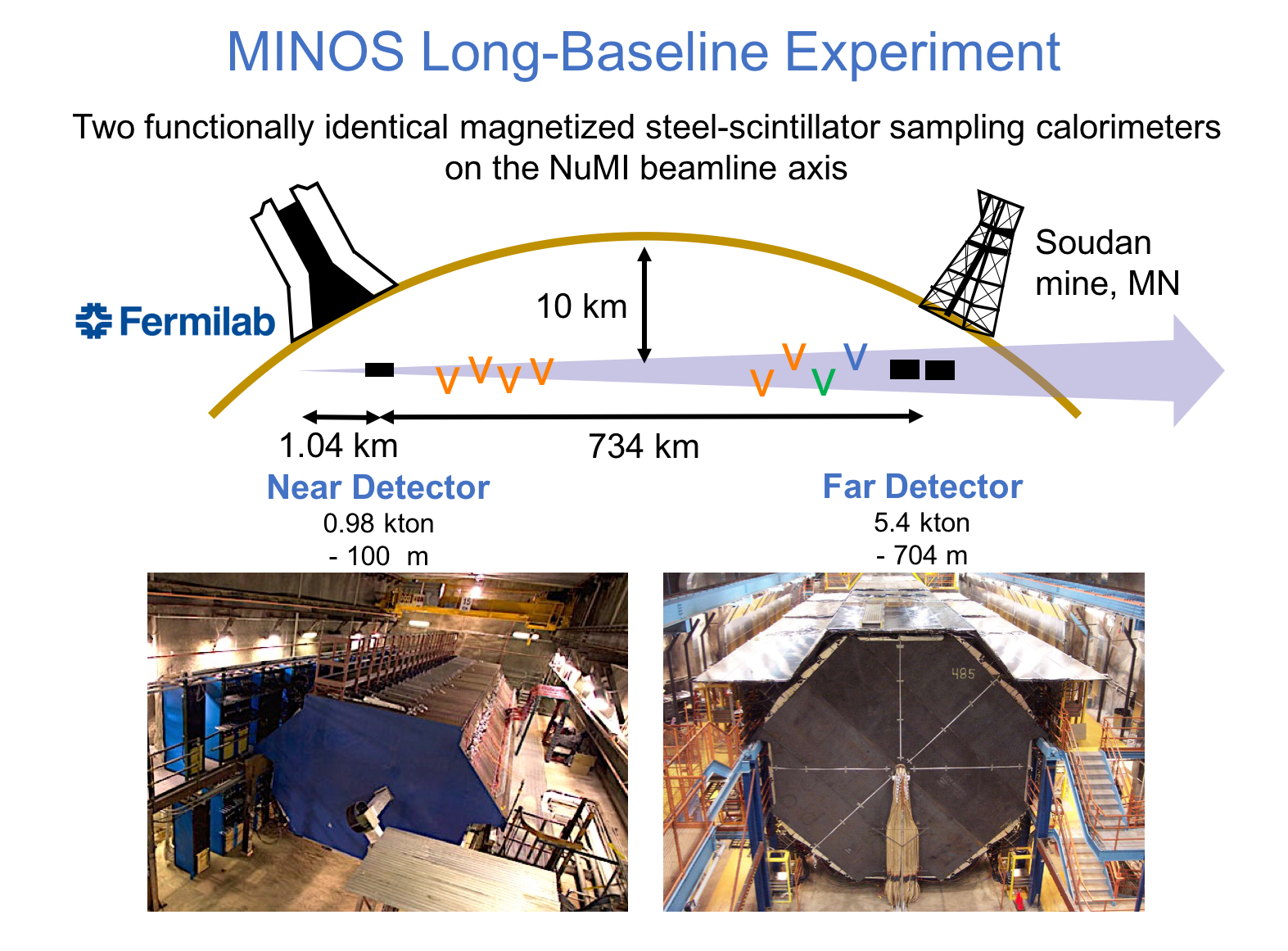
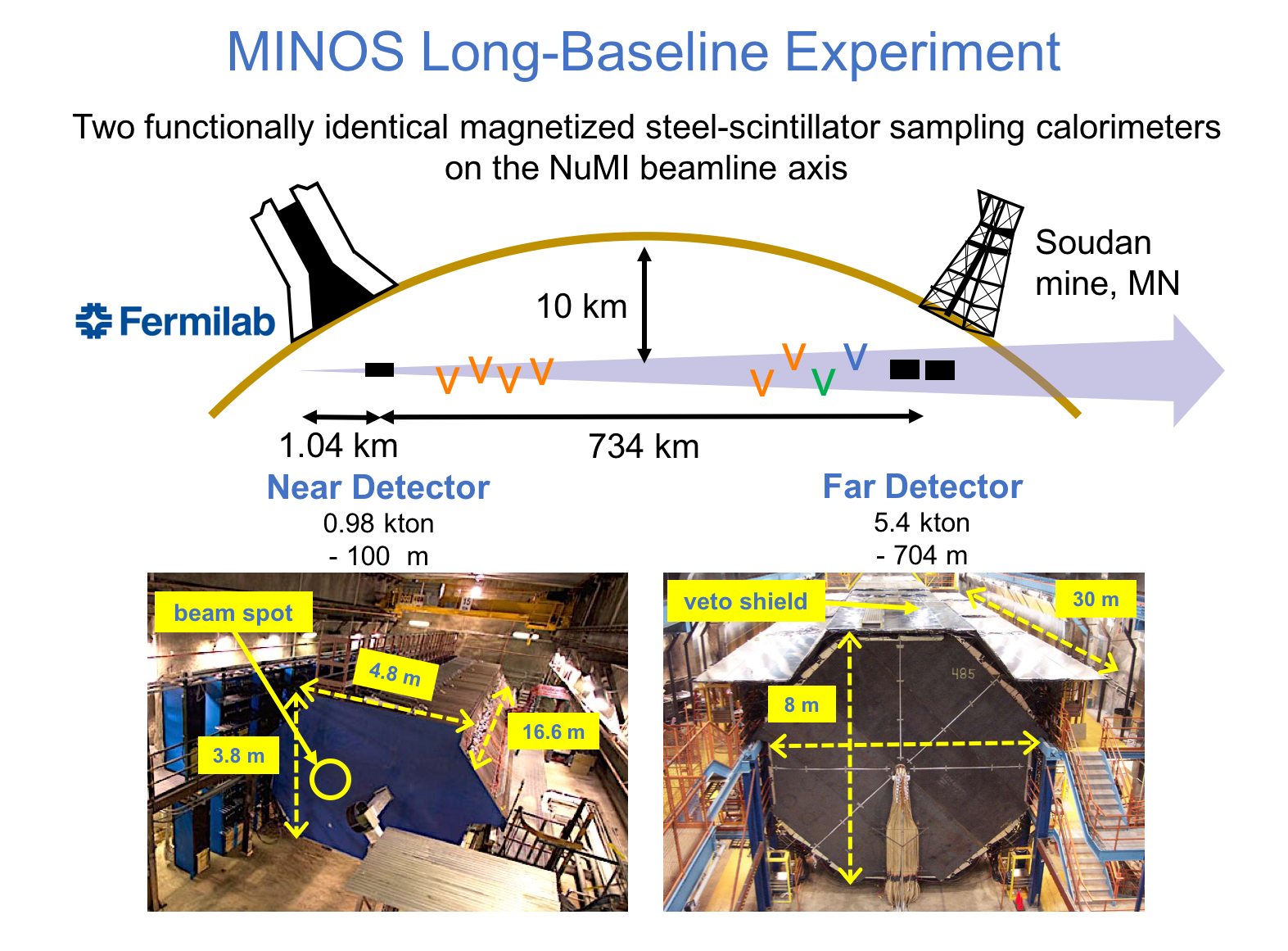
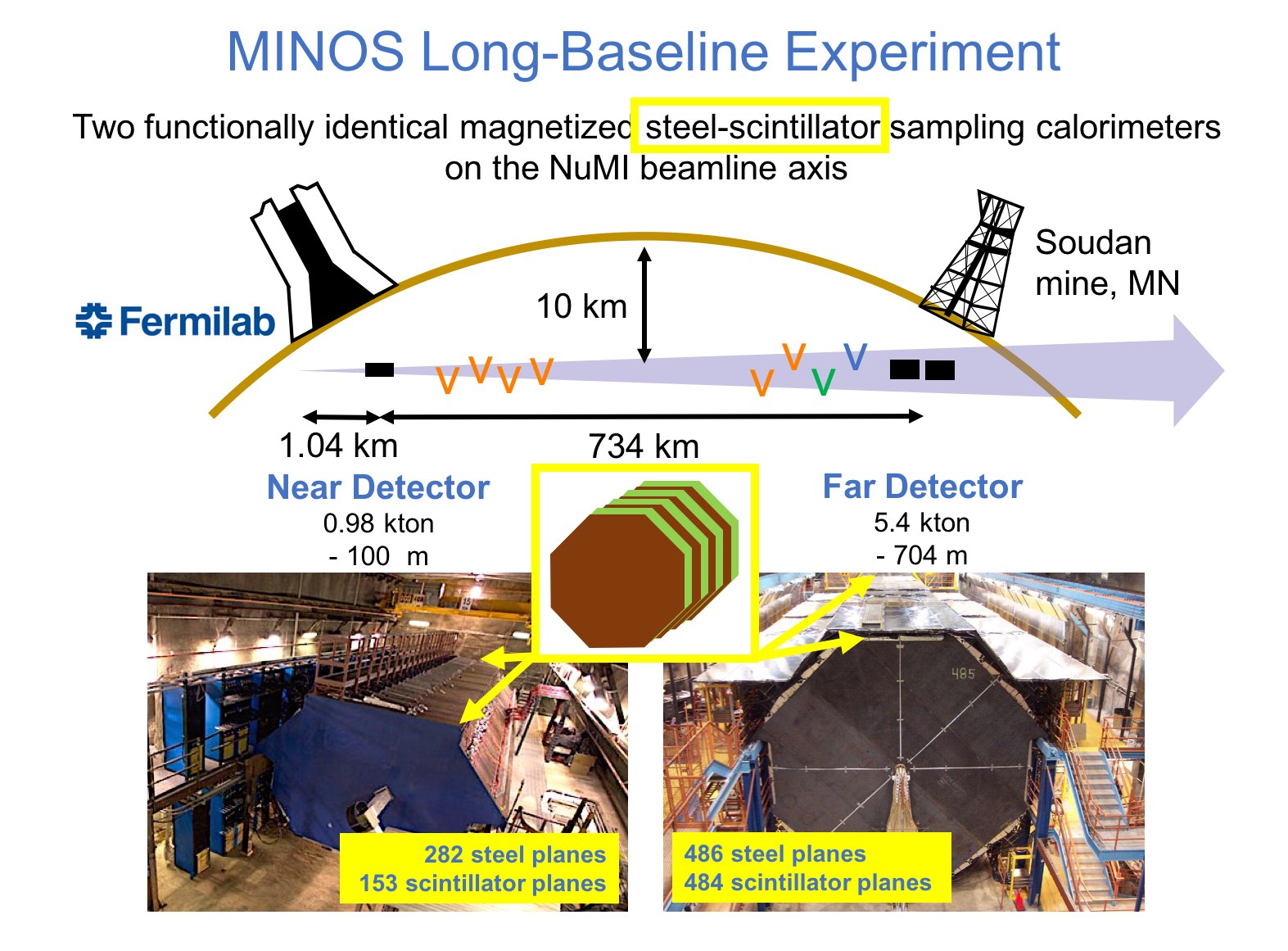
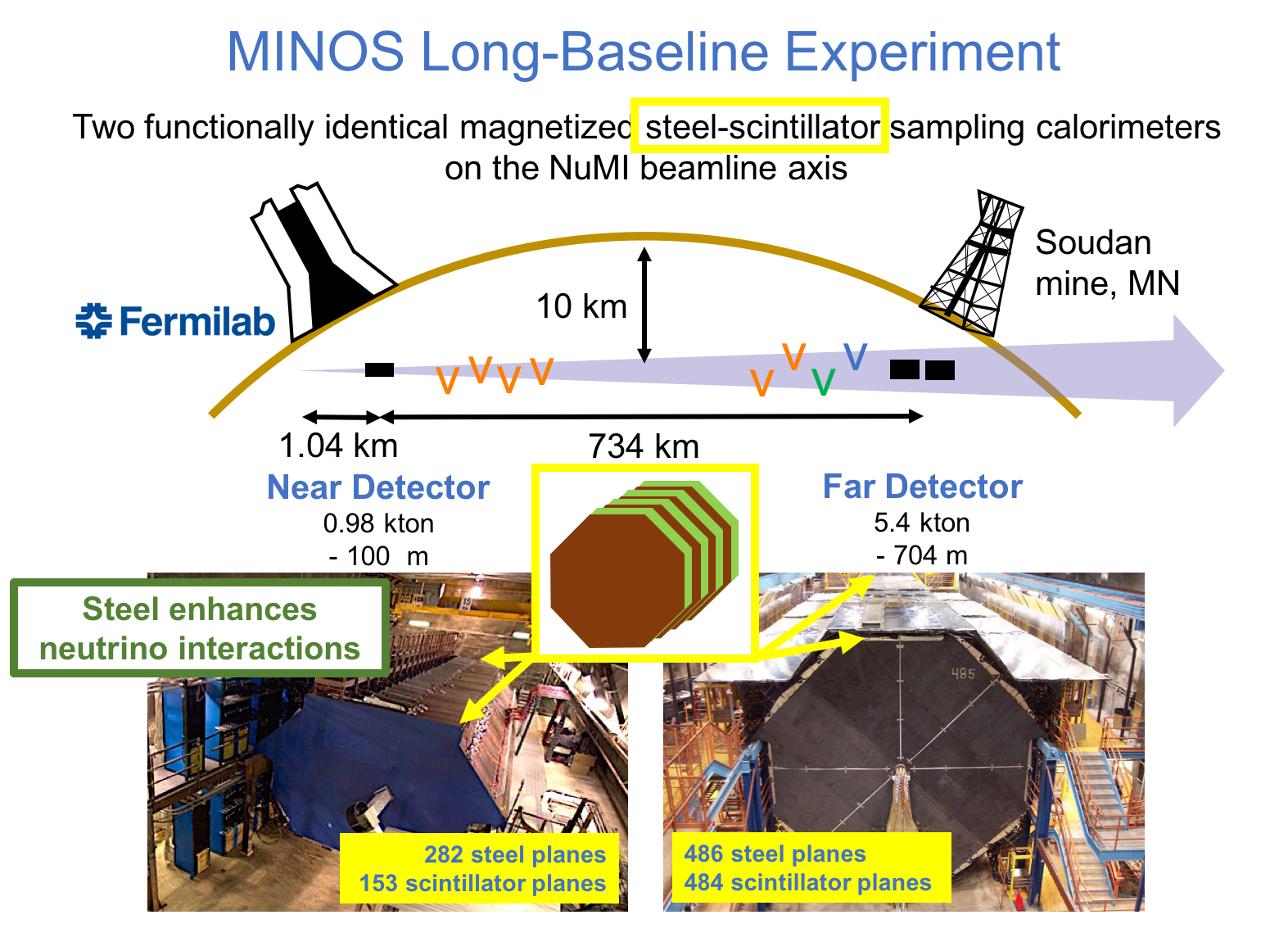
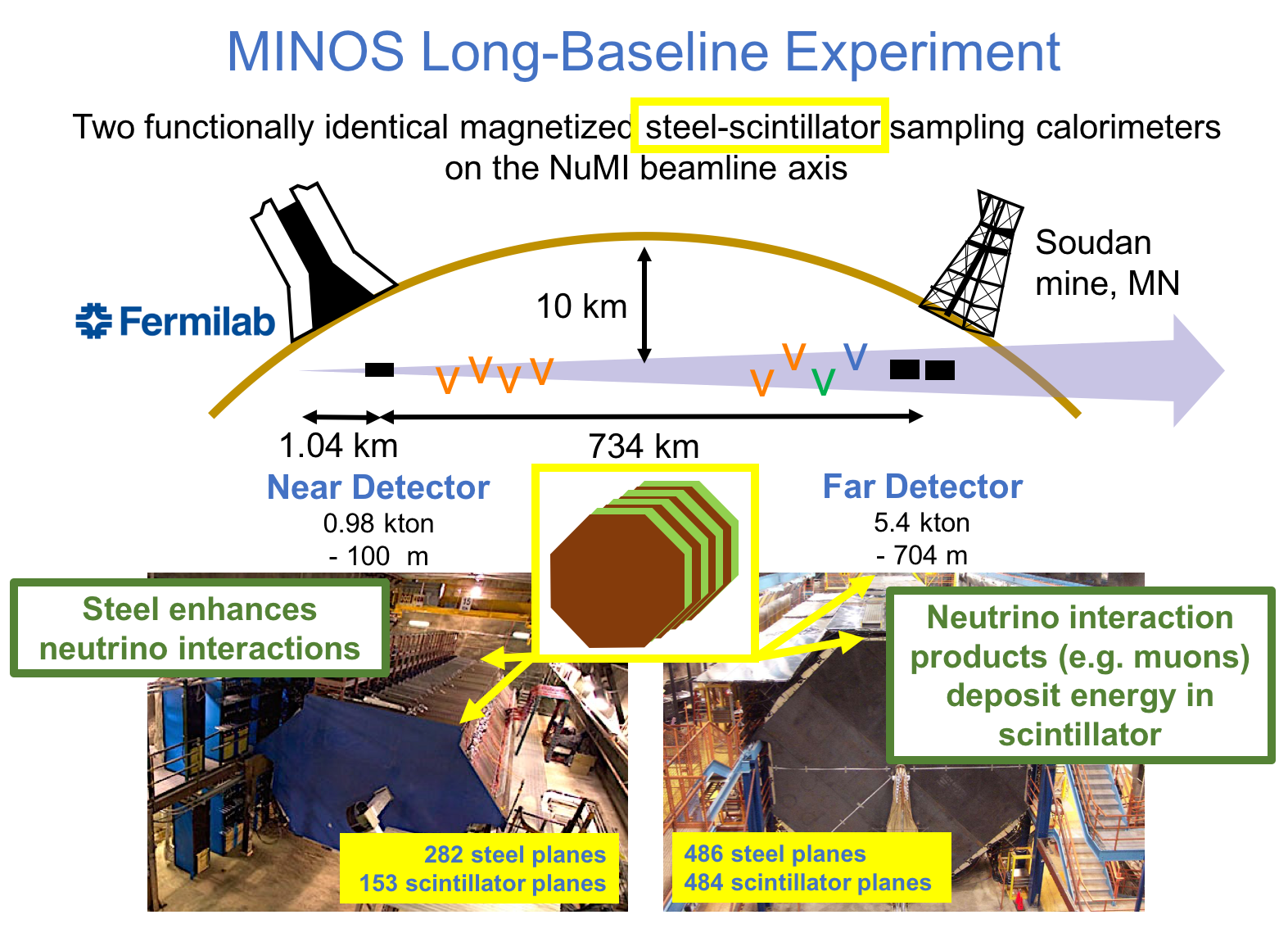
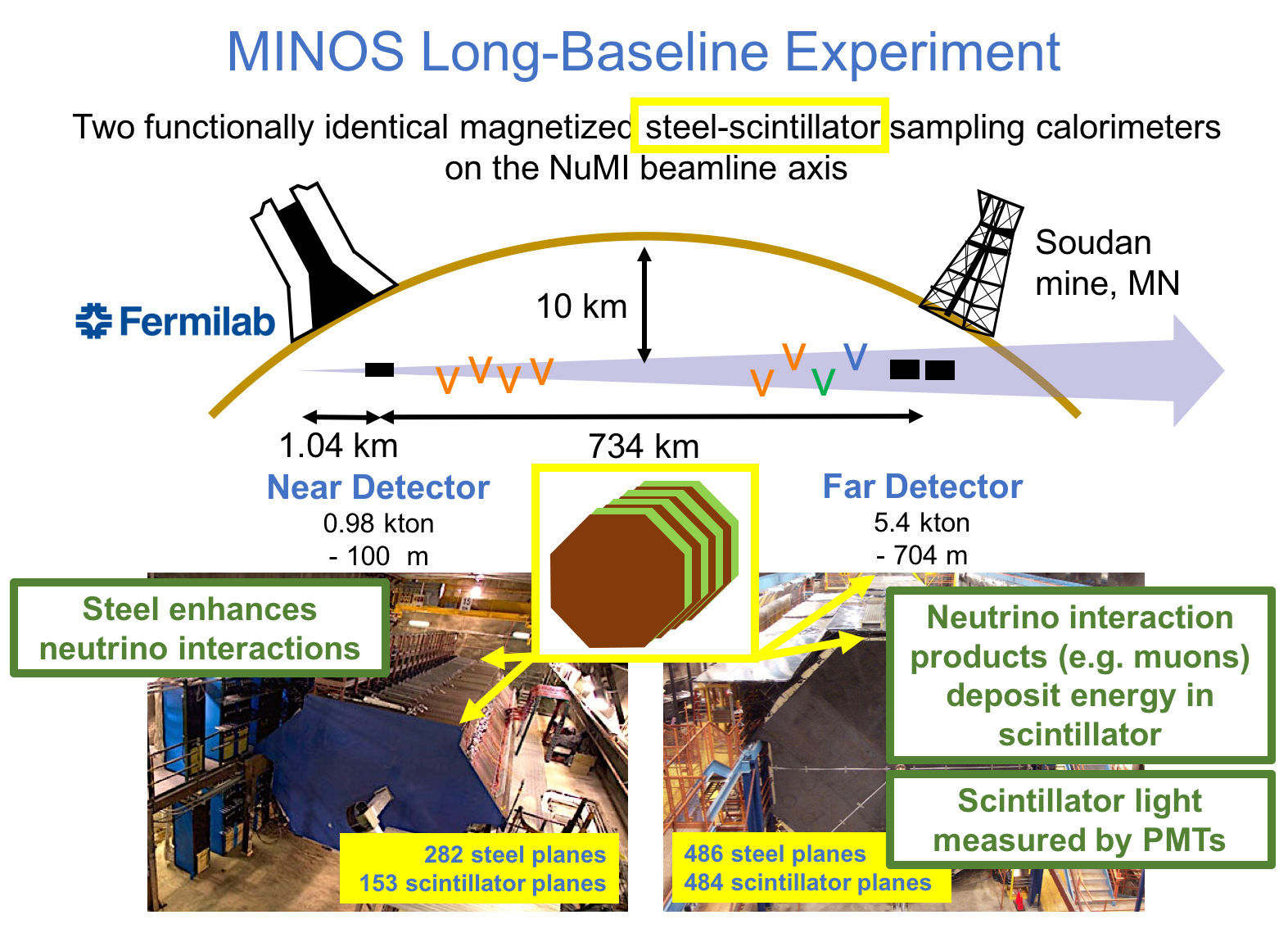
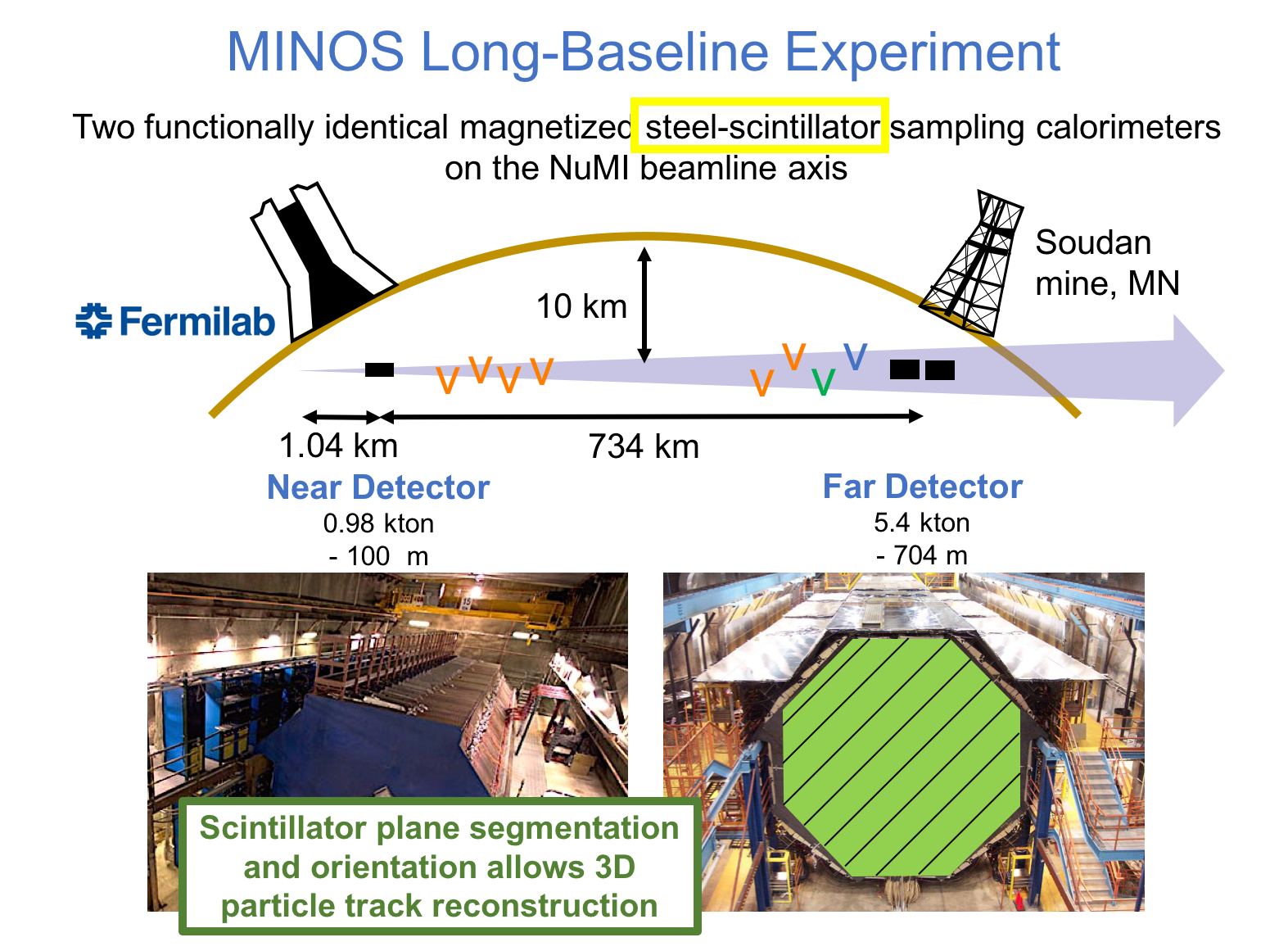
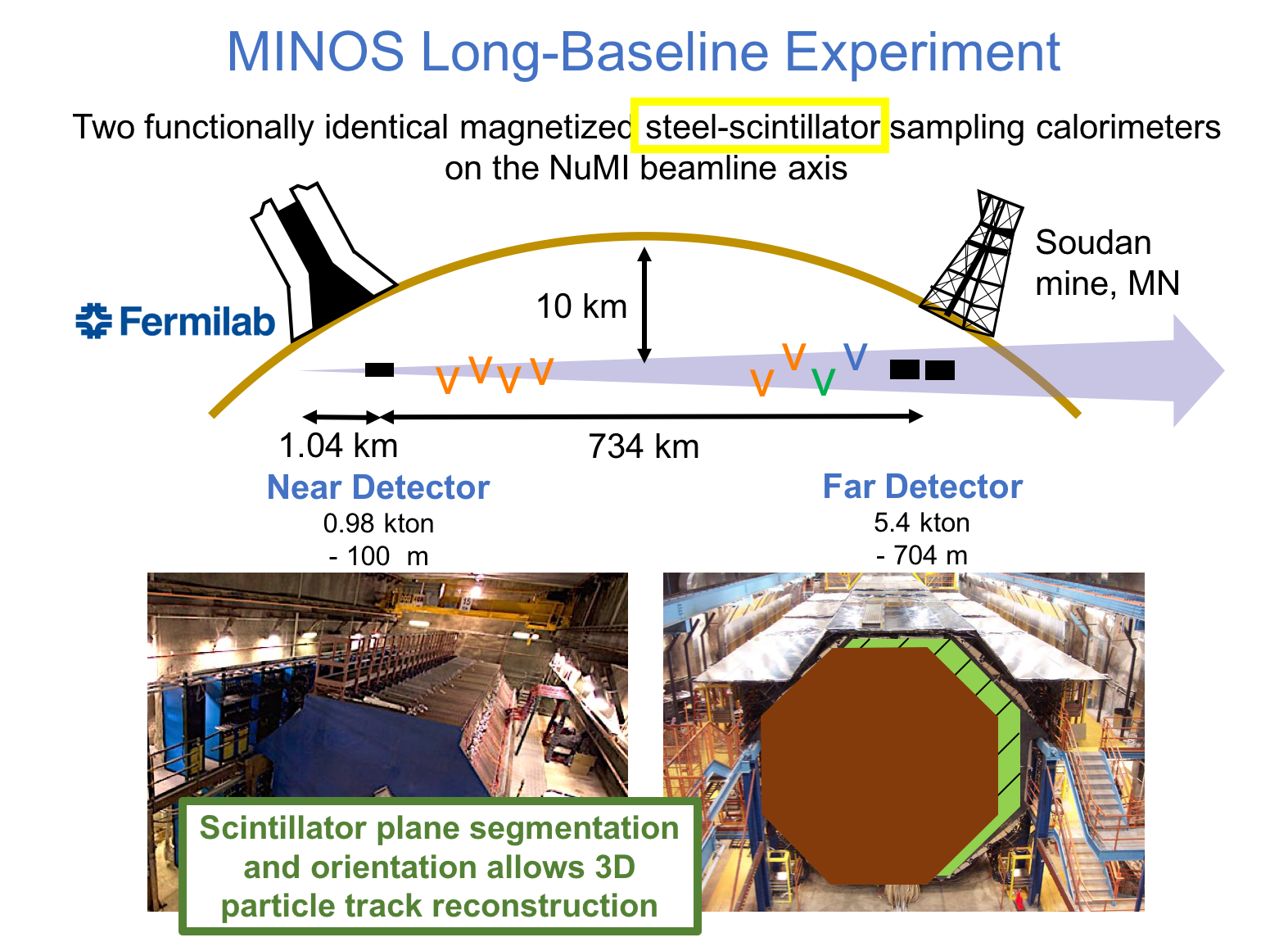
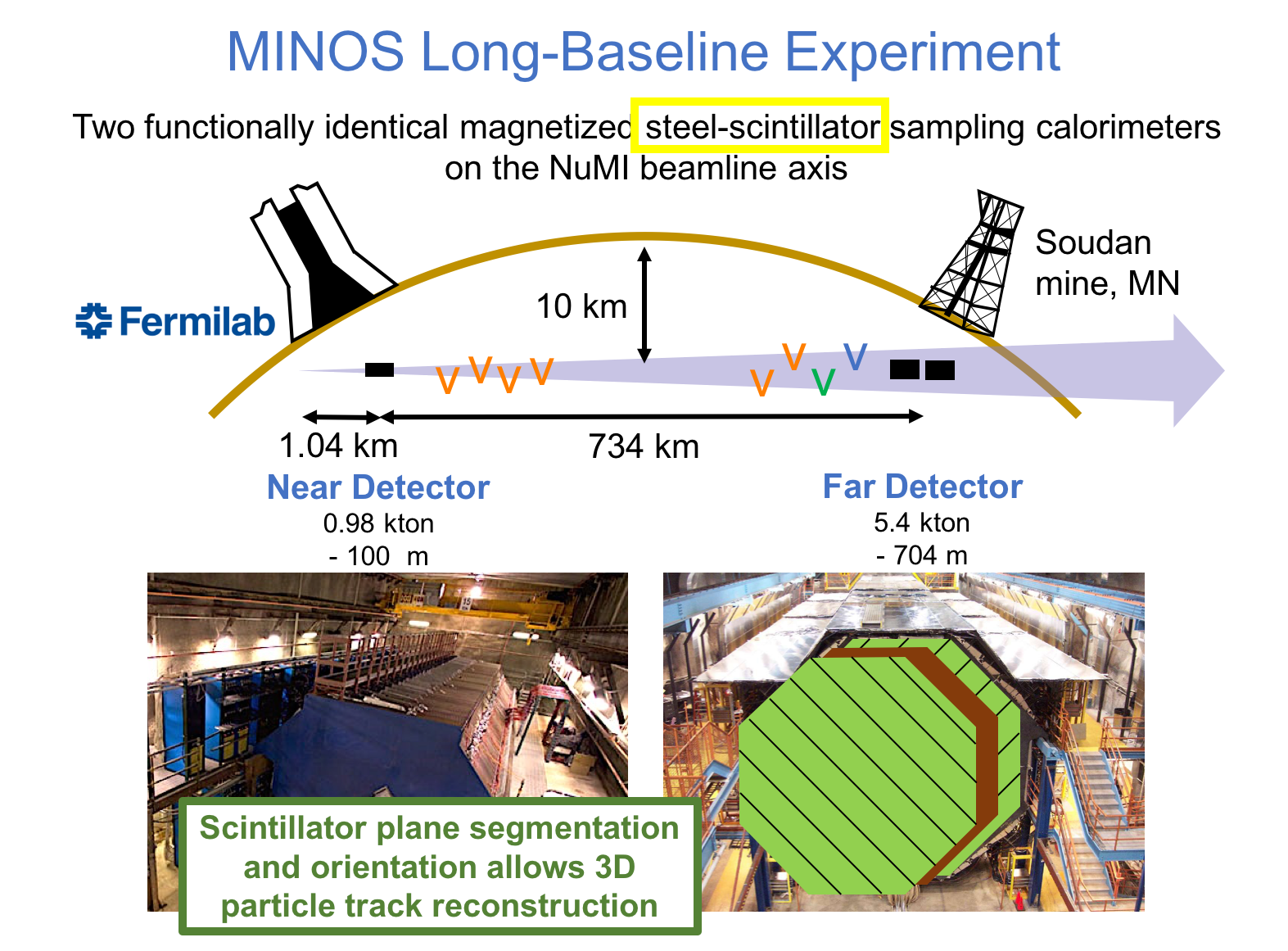
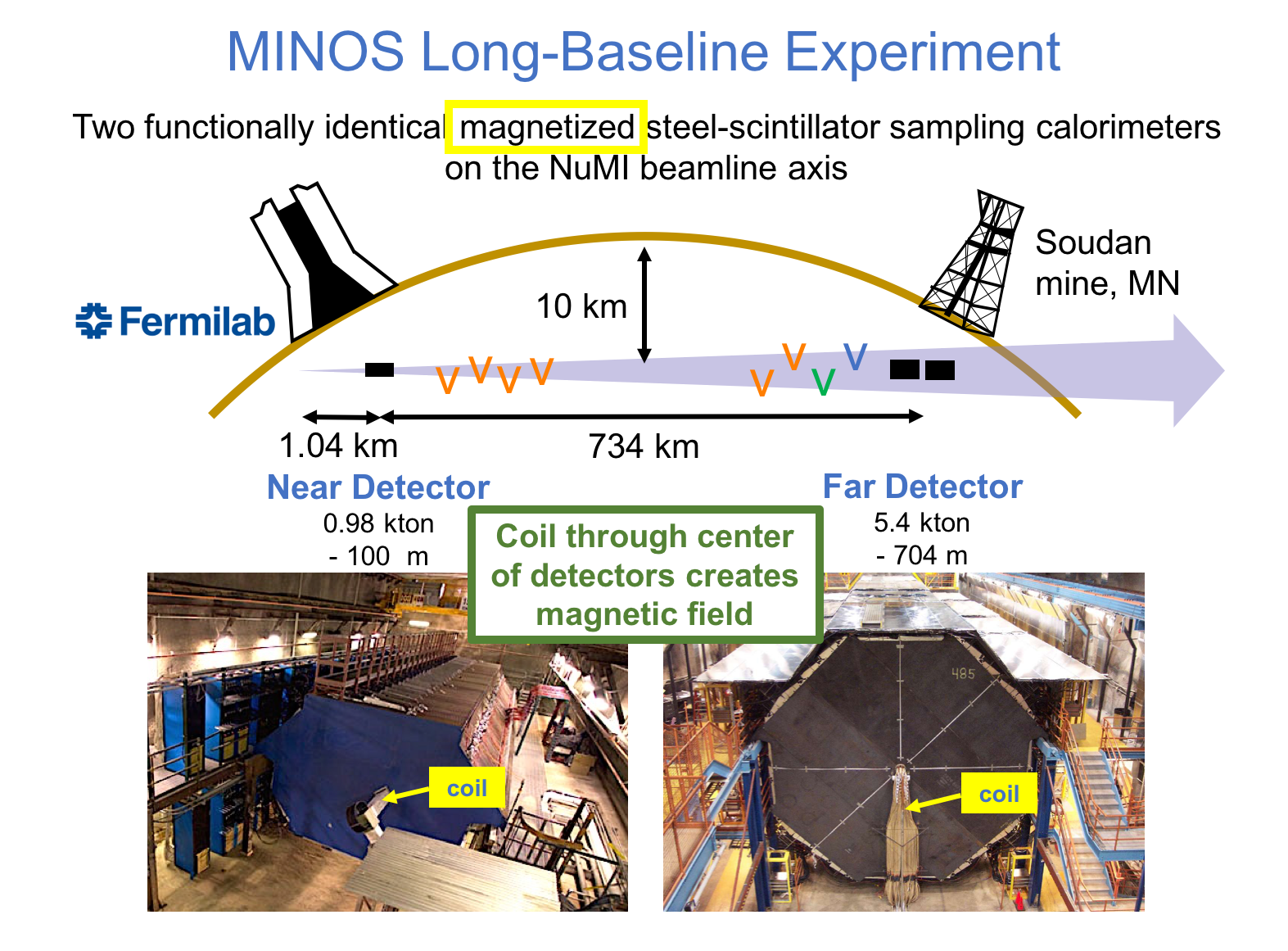
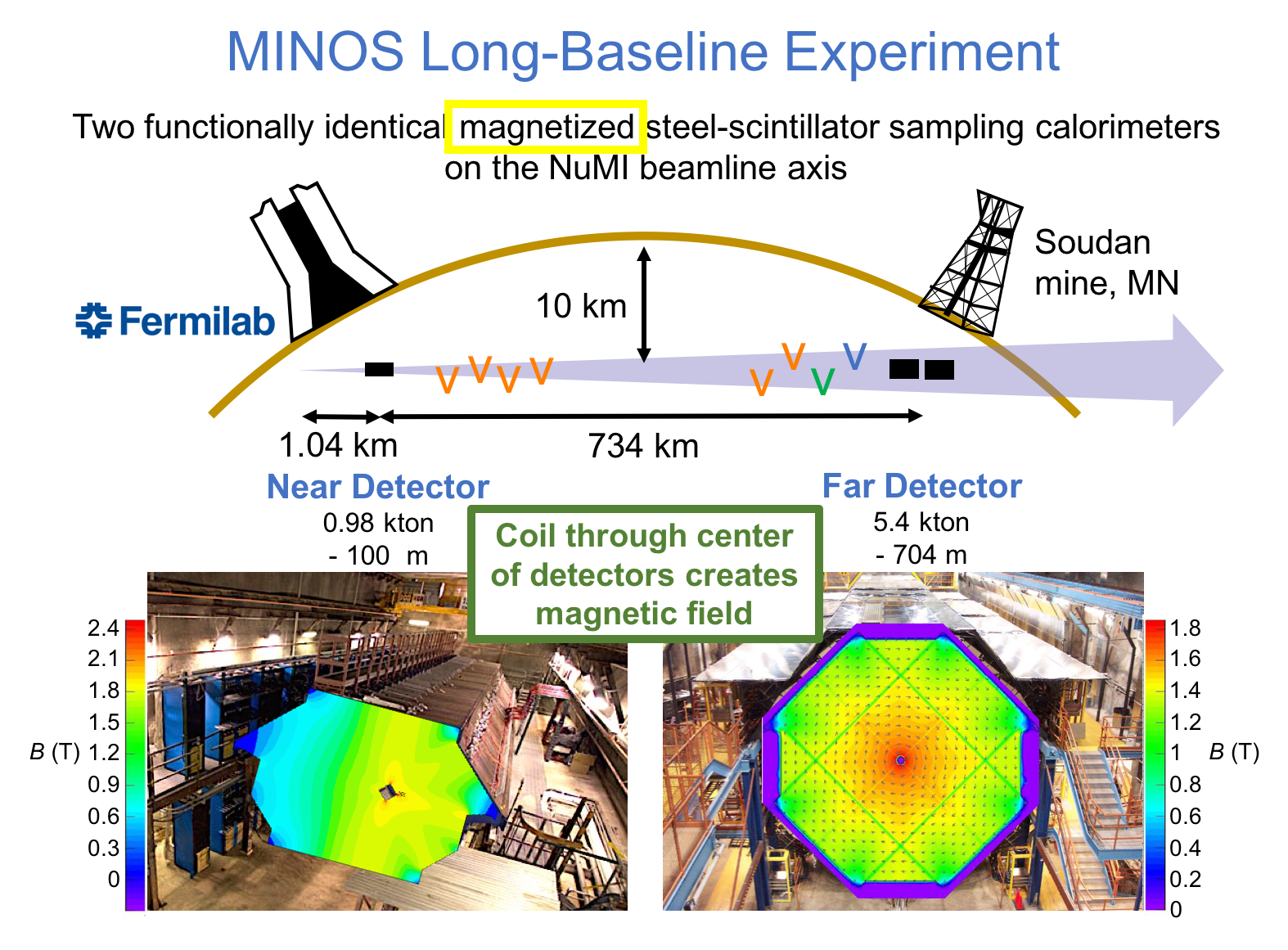
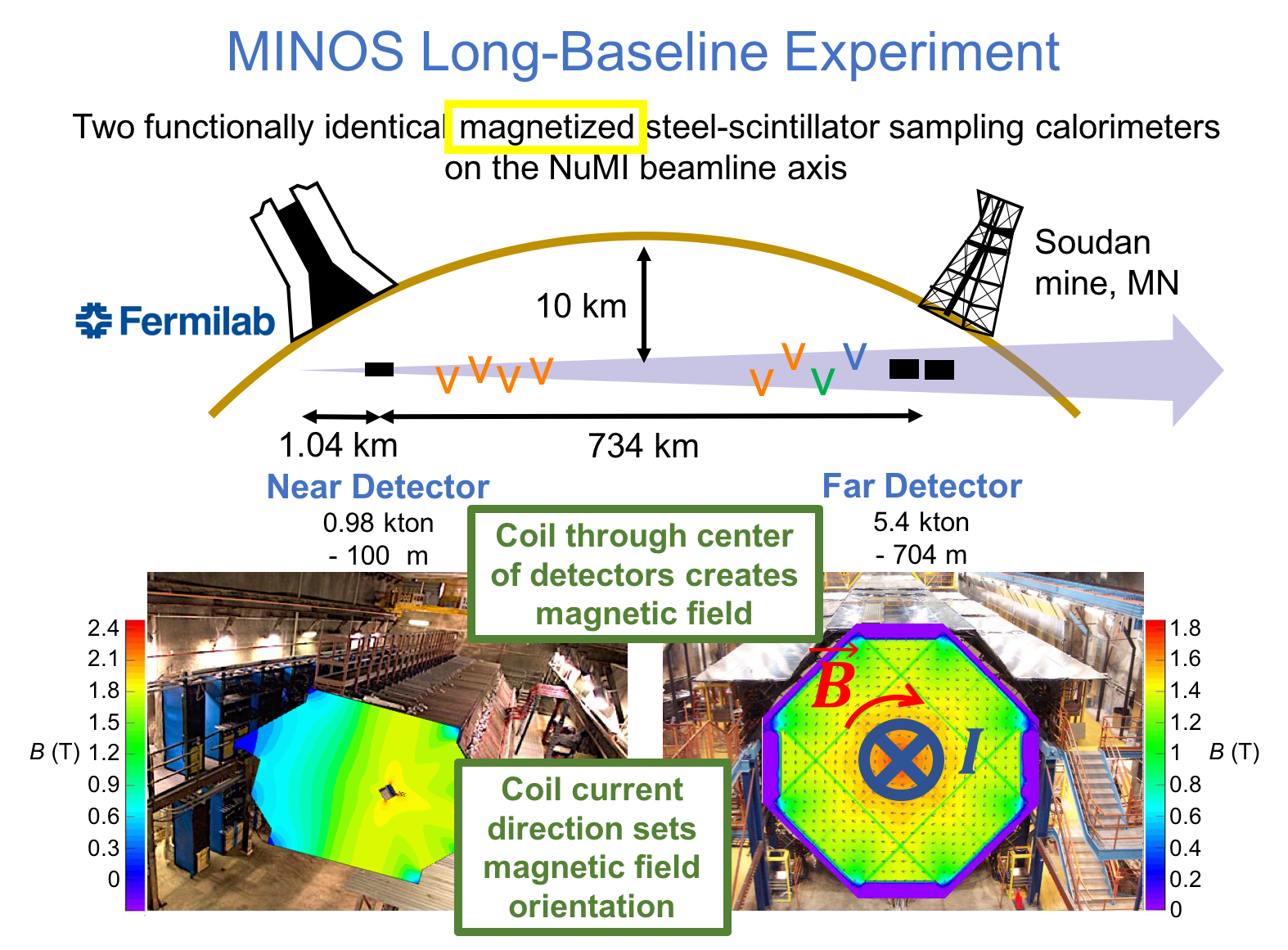
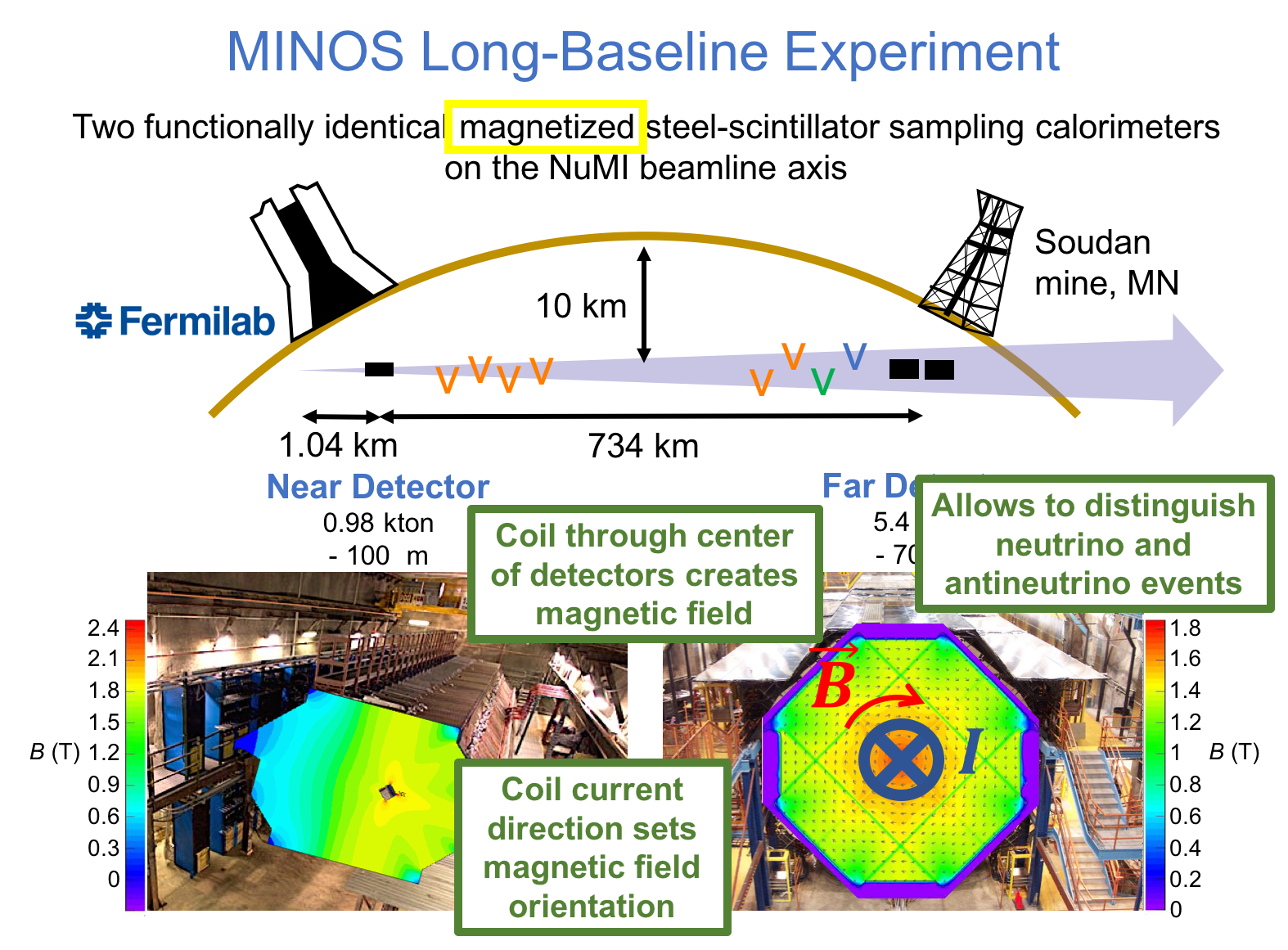
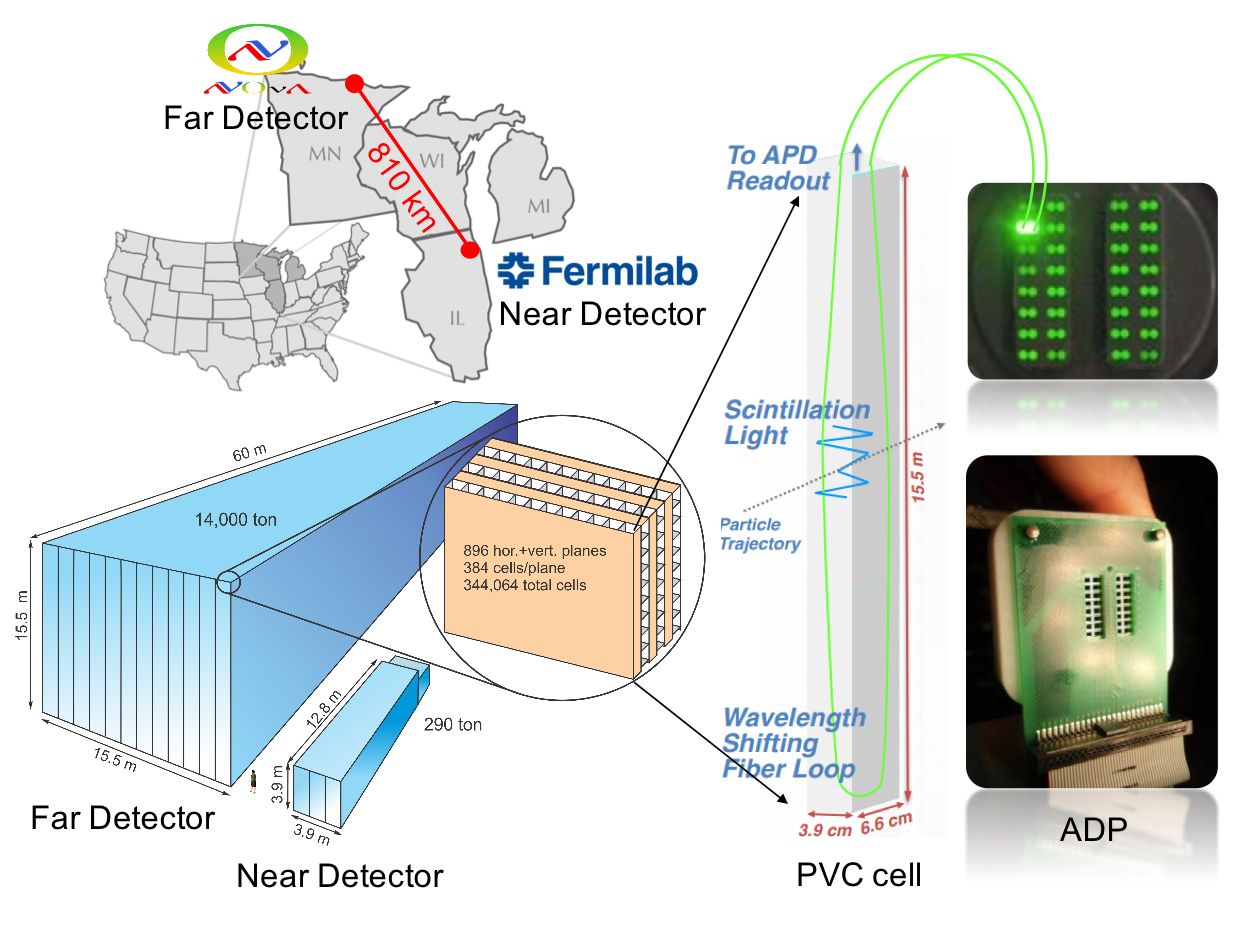
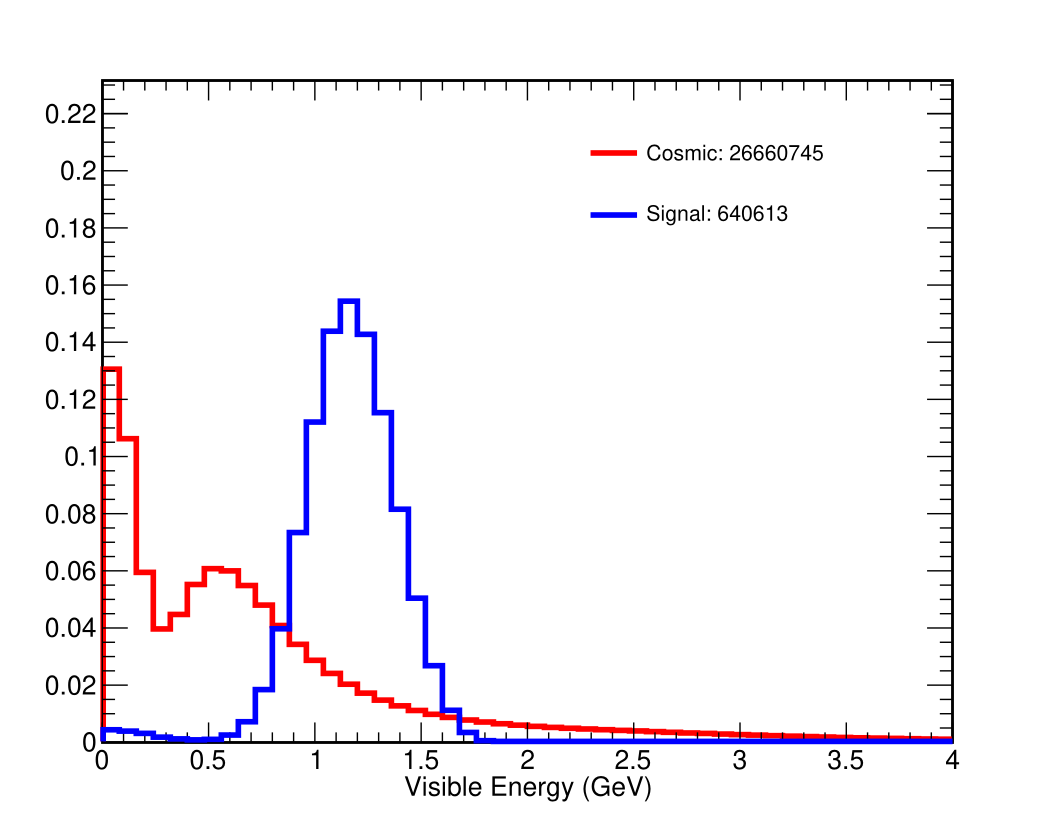
MINOS or Main Injector Neutrino scillation earch was an on-axis long-baseline neutrino oscillation experiment that was exposed to the the NuMI neutrino beam from Fermilab. It used a Near Detector (ND) with a mass of 0.98 $~$ metric-kiloton located 1.04 $~$ km from the NuMI target and a Far Detector (FD) with a mass of 5.4 $~$ metric-kiloton located 735 $~$ km from the target in the Soudan Underground Mine. These detectors were functionally equivalent magnetized steel-scintillator, tracking-sampling calorimeters. The detectors consisted of alternating planes of 2.54 $~$ cm thick steel plates and 1 $~$ cm thick polystyrene-based (plastic) scintillator strips. The scintillation light resulting from particle interactions, following the initial neutrino interaction was collected and guided by wavelength-shifting (WLS) fibers to photomultipliers (PMTs). The PMT signals were used to determine the flavor and energy of the interacting neutrino. Each detector was magnetized by a coil that ran through the center of the detector, parallel to its length. The magnetic field allowed the MINOS detectors to distinguish between $\nu_\mu$ and $\overline{\nu}_\mu$ charged-current (CC) interactions based on the curvature of the resulting muon. The ND was used to monitor the neutrino beam before significant neutrino oscillations take place. The FD was used to measure the deficit in neutrino events due to oscillations occurring along the way from Fermilab to Soudan, a trip that takes less than 3 milliseconds for these neutrinos. Fig. 1 and Fig. 2 illustrate the basic design of the MINOS detectors.

Figure 1: Flip through the images, by clicking on the left or the right of each figure or using the indicator located on top, to learn more about the MINOS detectors.

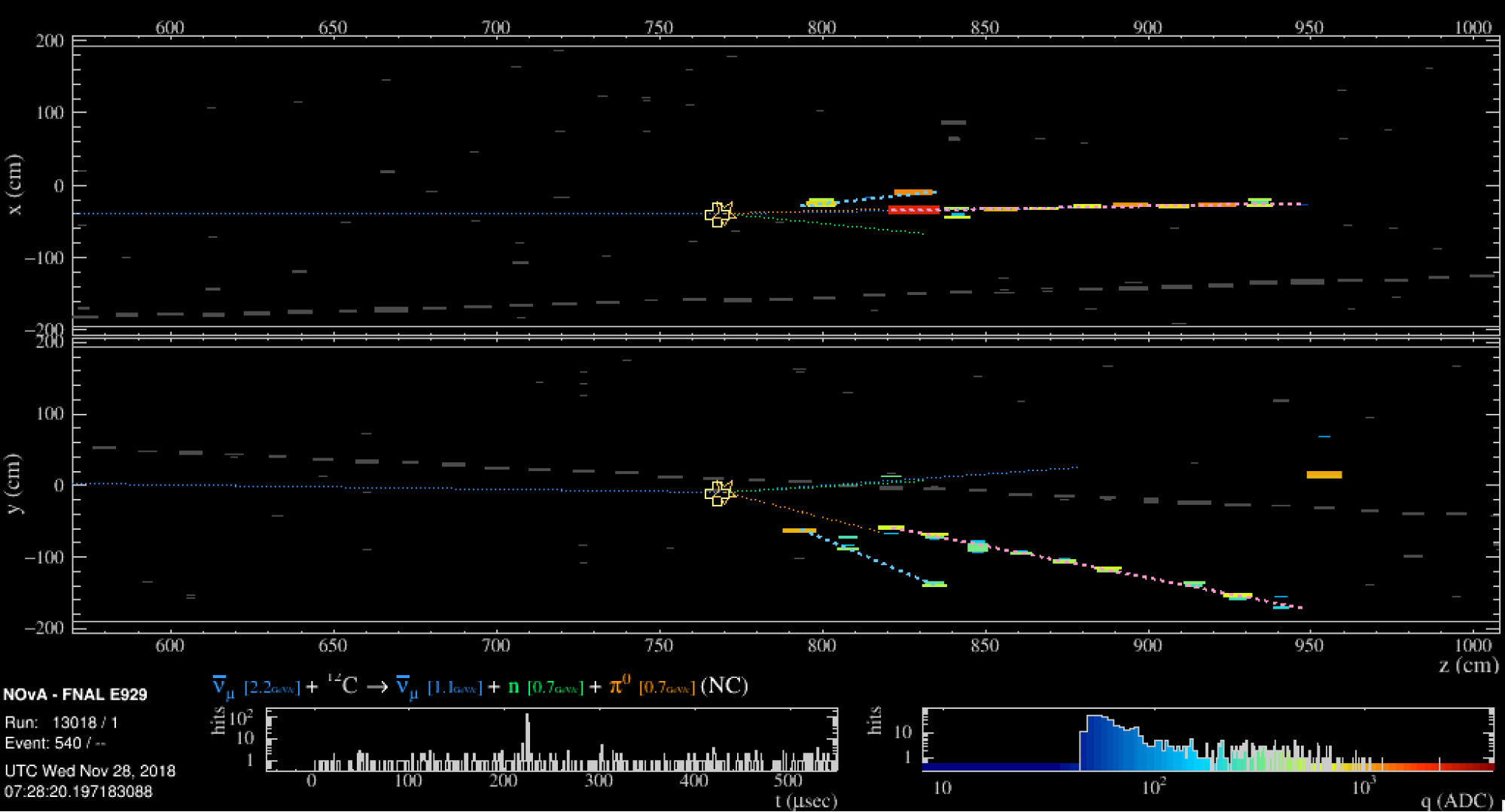
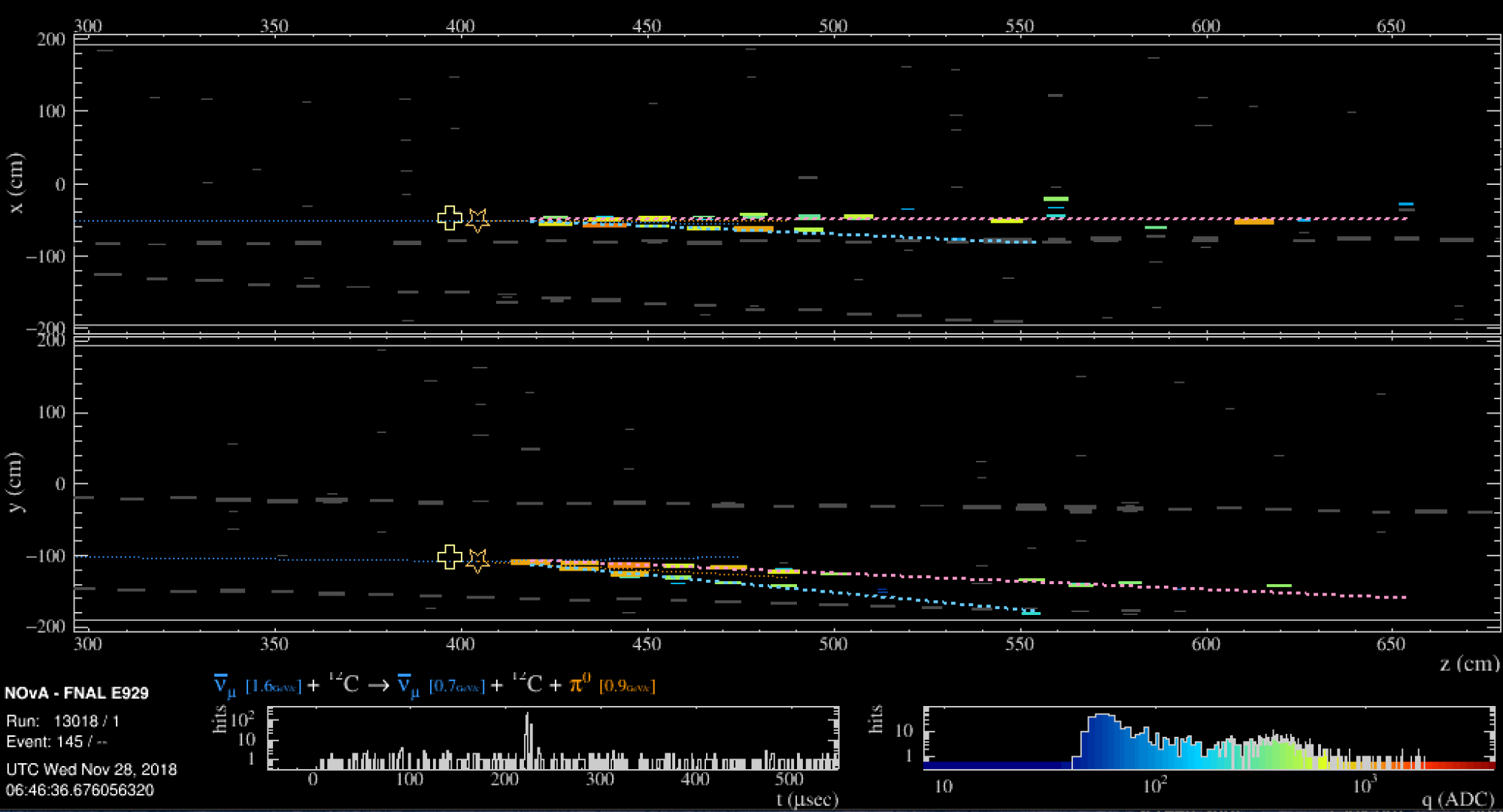
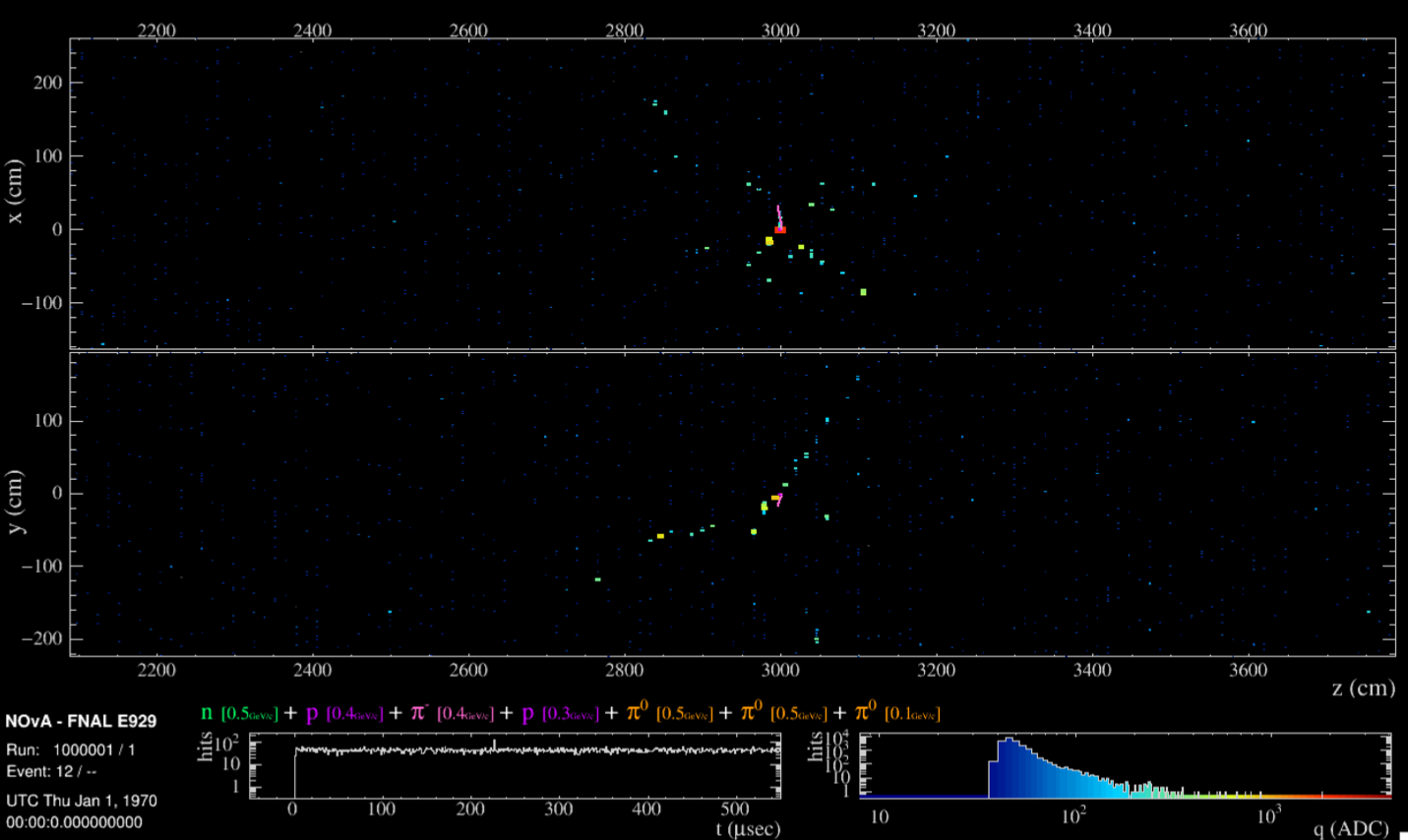
Figure 2: Flip through the images, by clicking on the left or the right of each figure or using the indicator located on top, to learn more about the MINOS readout system.

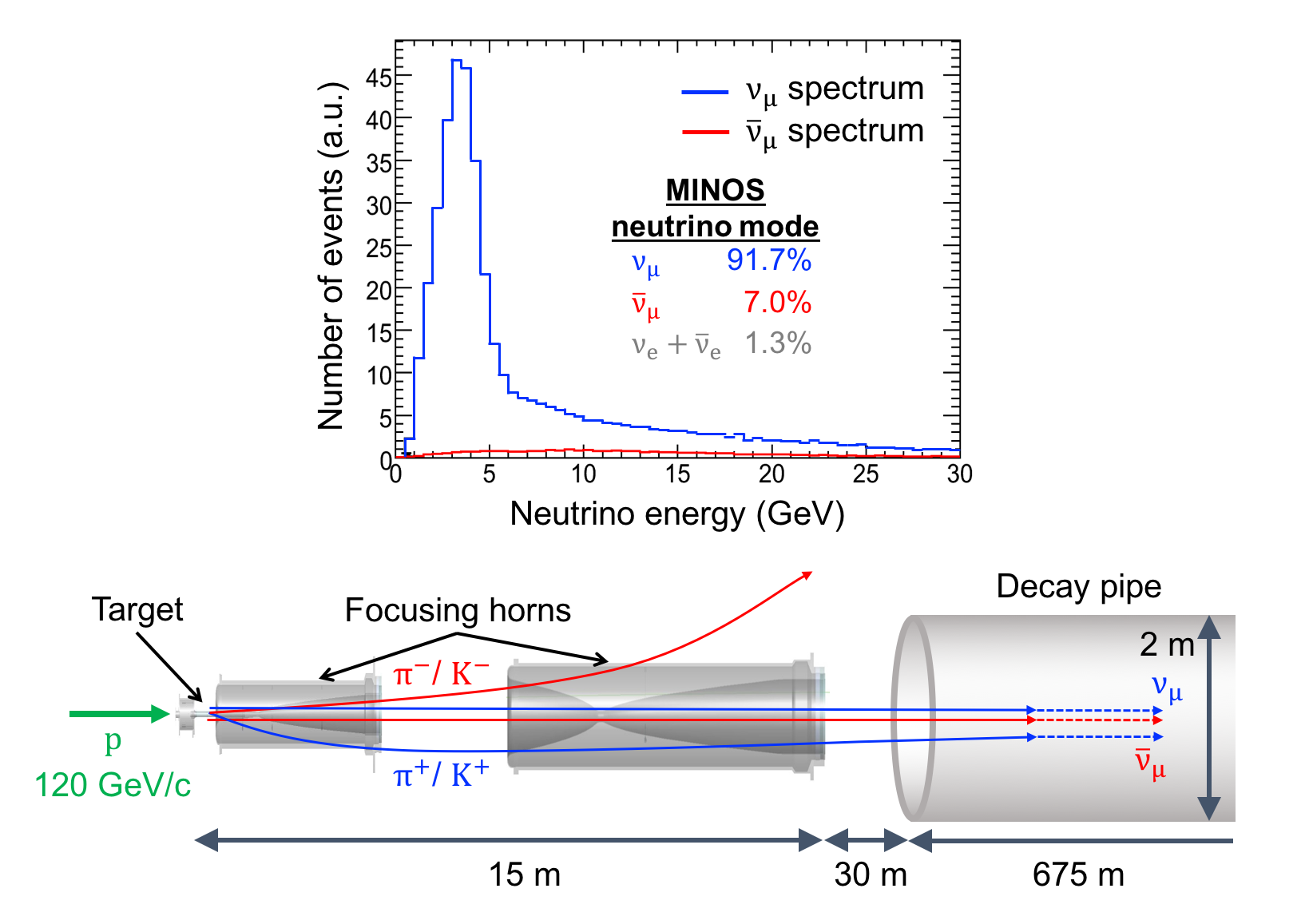
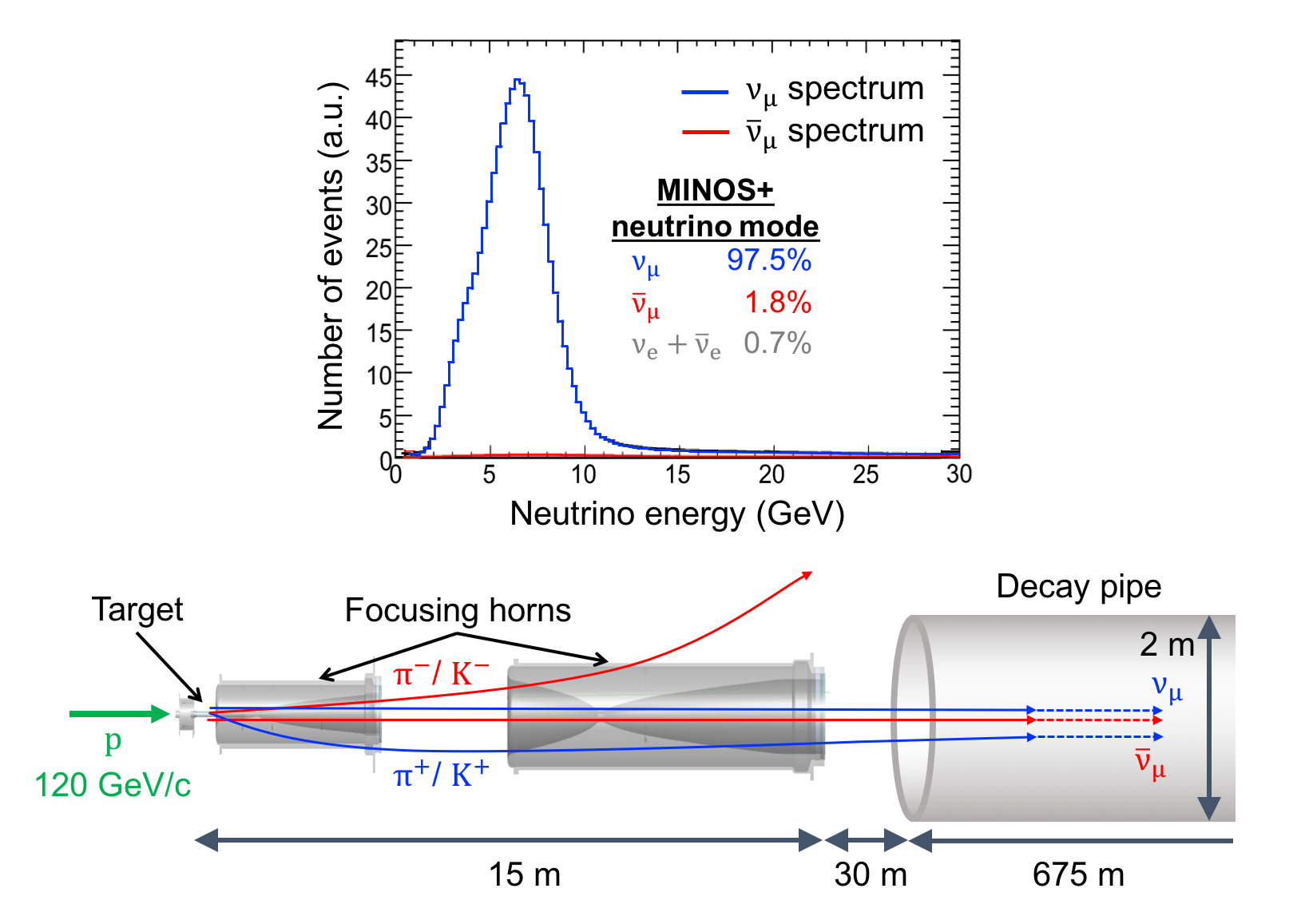
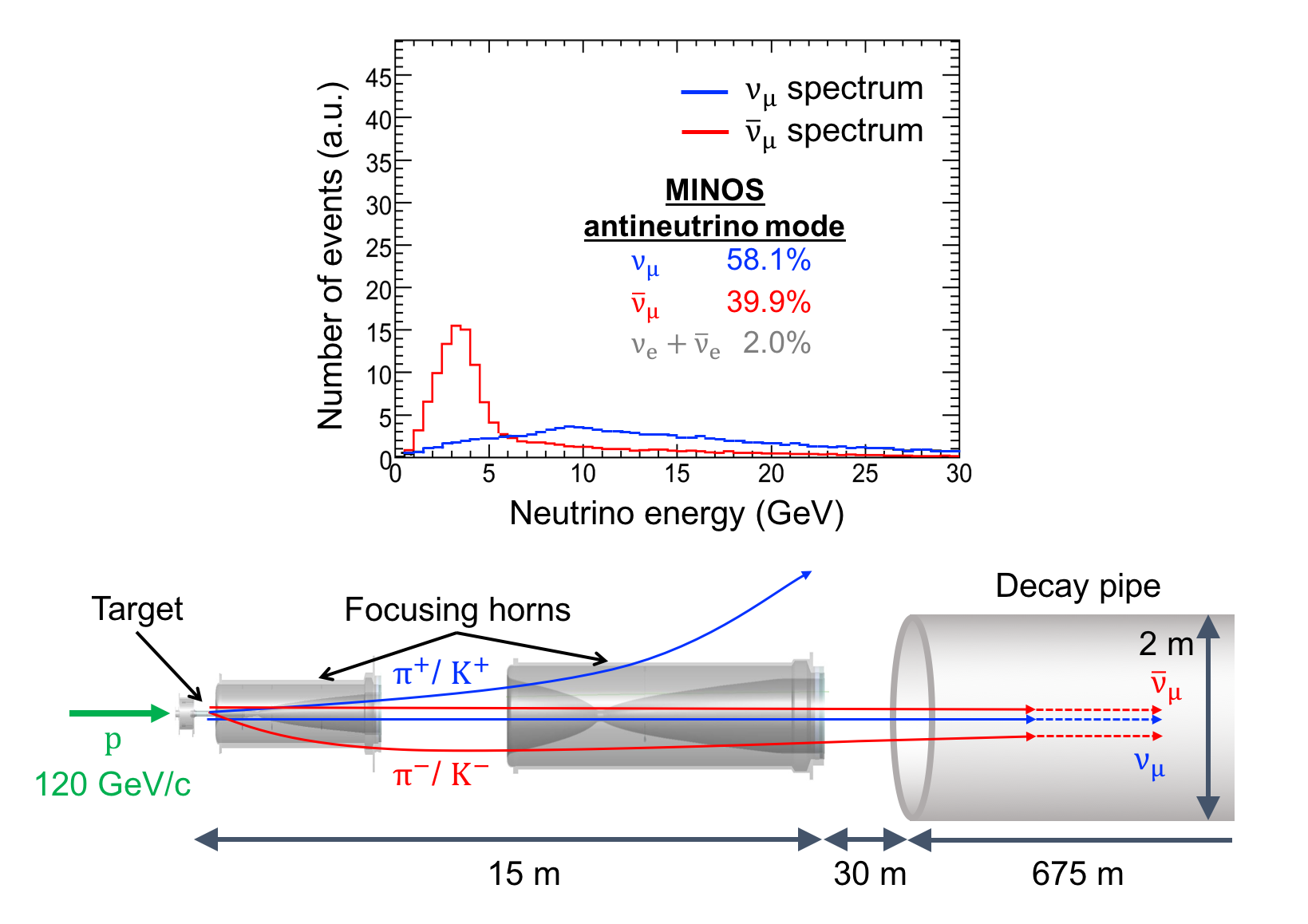
The NuMI beam is produced by colliding 120 $~$ GeV protons into a graphite target. The resulting pions and kaons are then focused by two magnetic horns into a decay pipe, where they decay into muon (anti)neutrinos. The magnetic horns allow the beam to be operated in either a $\nu_\mu$ or $\overline{\nu}_\mu$ mode, as shown in Fig. 3. In June 2016 the NuMI beam achieved a beam power of 700 $~$ kW making it the most powerful neutrino beamline, currently used for the NO $\nu$ A experiment (see below).

Figure 3: Creating a muon neutrino or antineutrino beam with NuMI. Positive and negative pions and kaons resulting from protons interacting with the NuMI target are either focused or defocused by the magnetic horns, depending on the direction of the current running through the horns. When positive pions and kaons are focused into the decay pipe, their decays lead to a neutrino beam dominated by muon neutrinos (first figure for MINOS and second figure for MINOS+). Focusing negative pions and kaons leads to a neutrino beam dominated by muon antineutrinos (third figure).

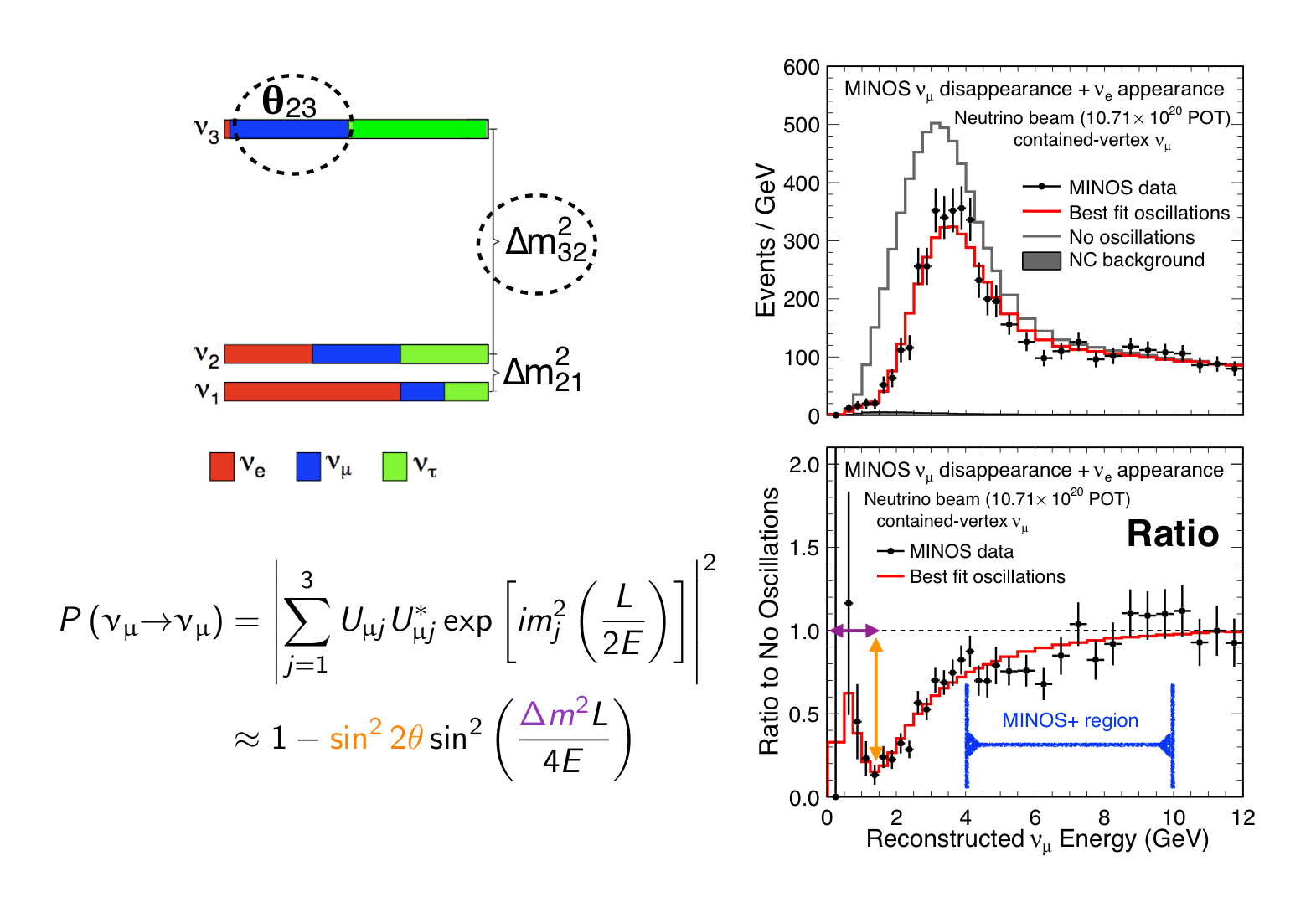
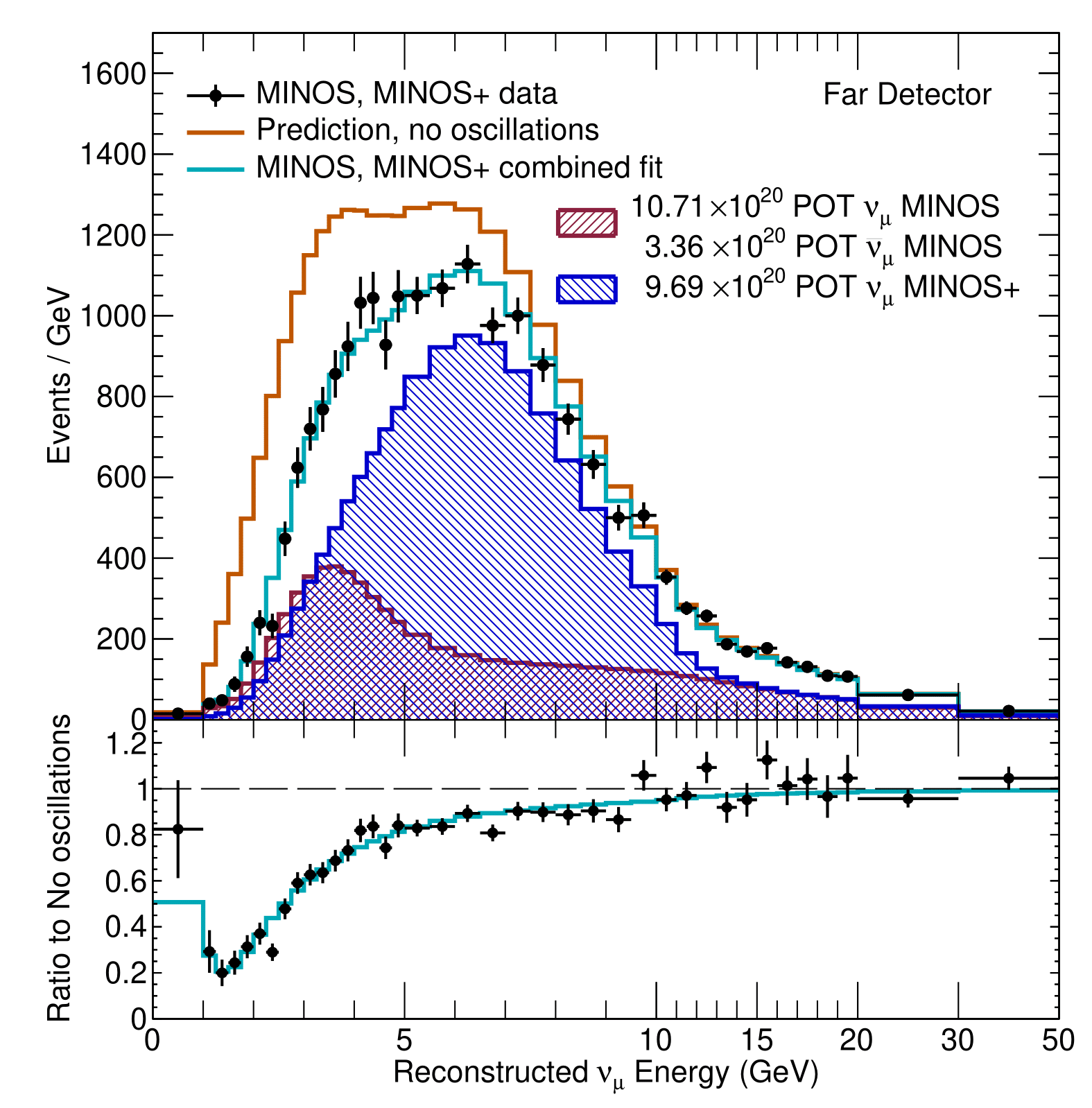
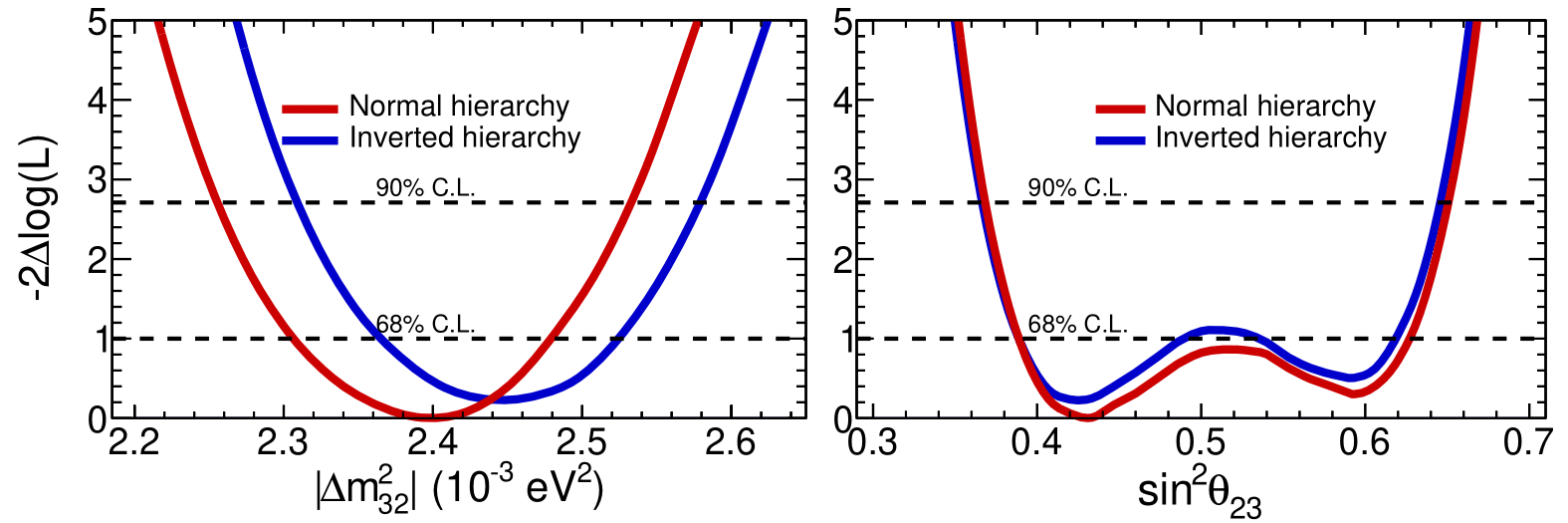
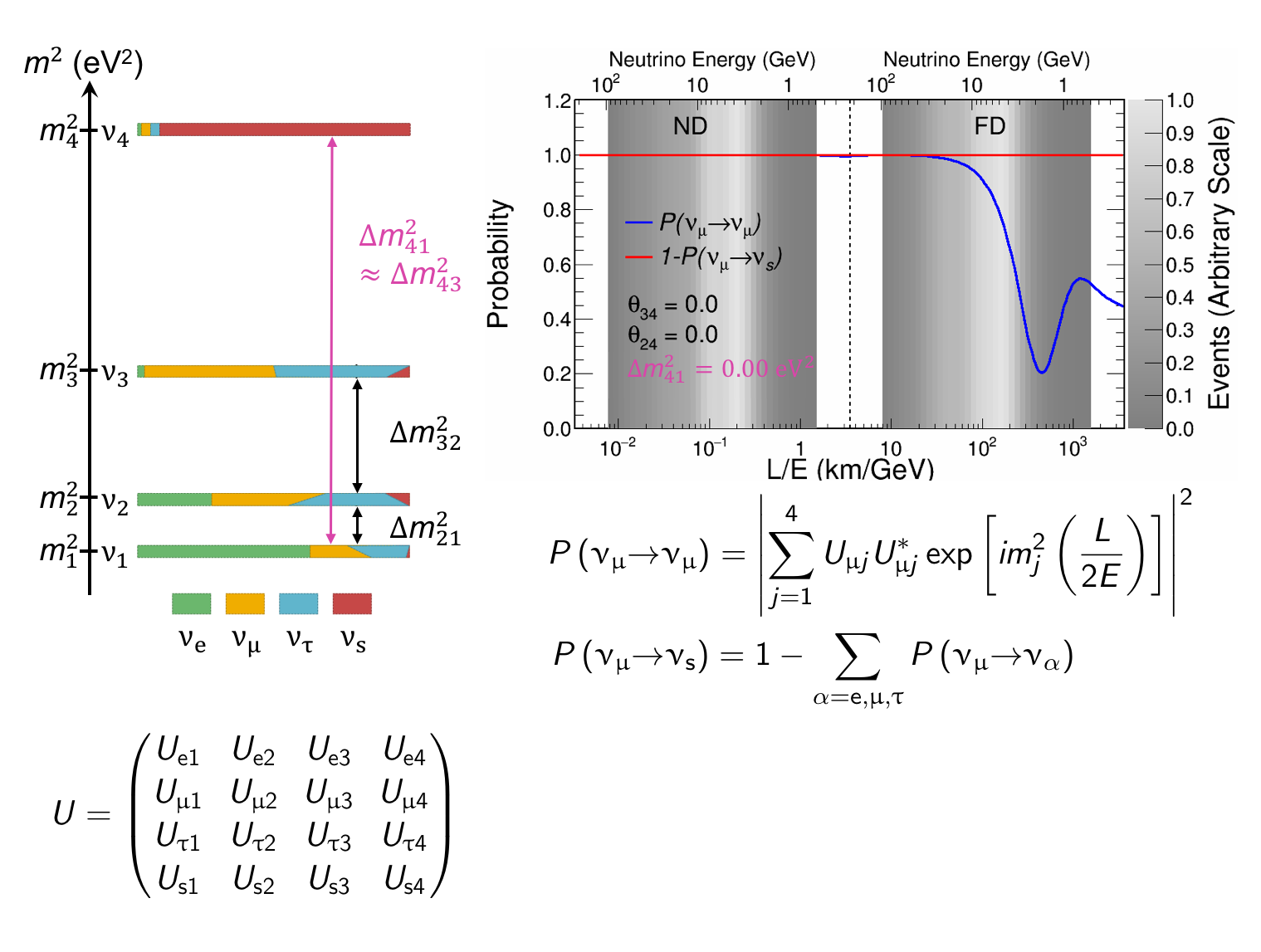
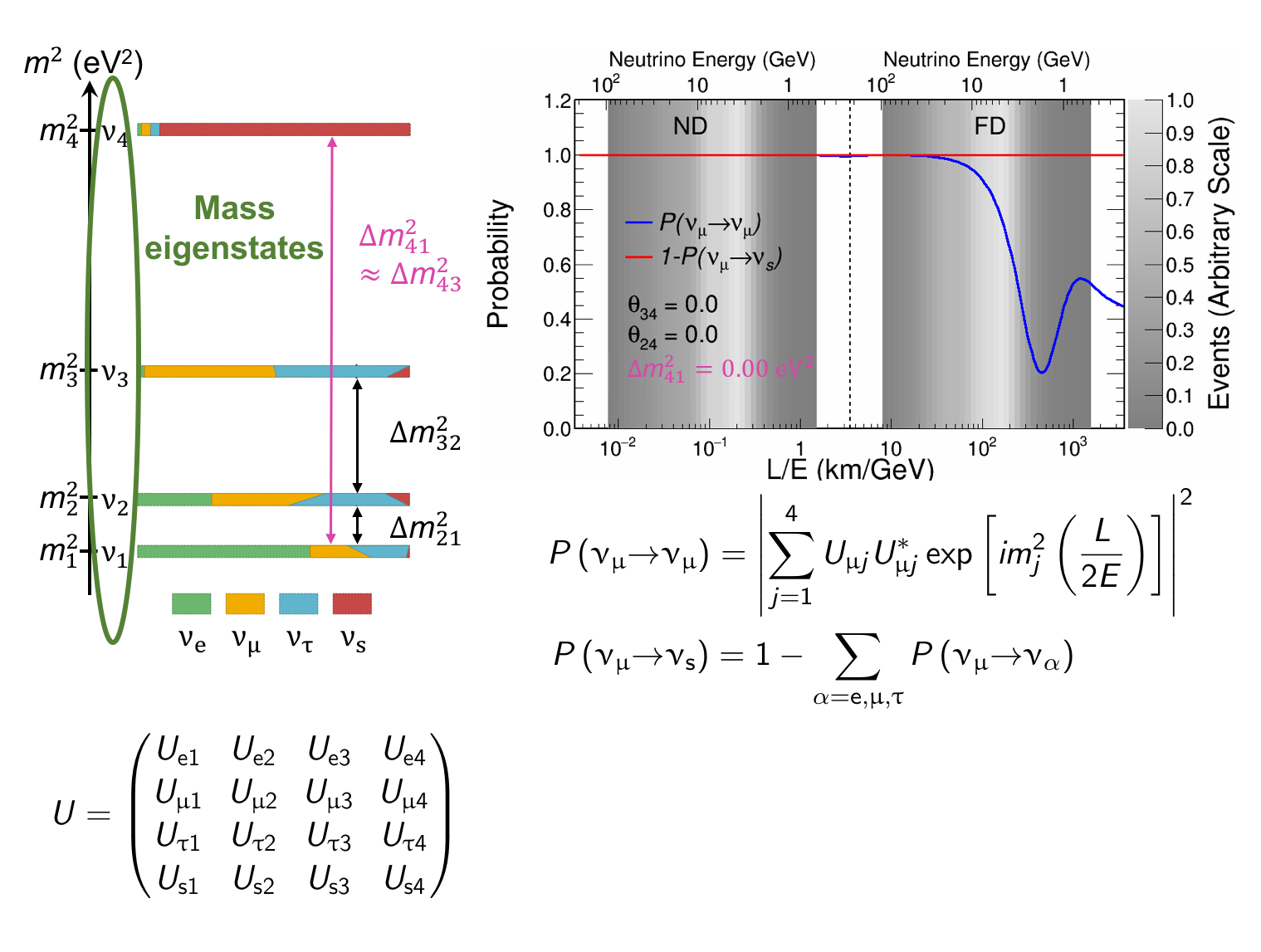
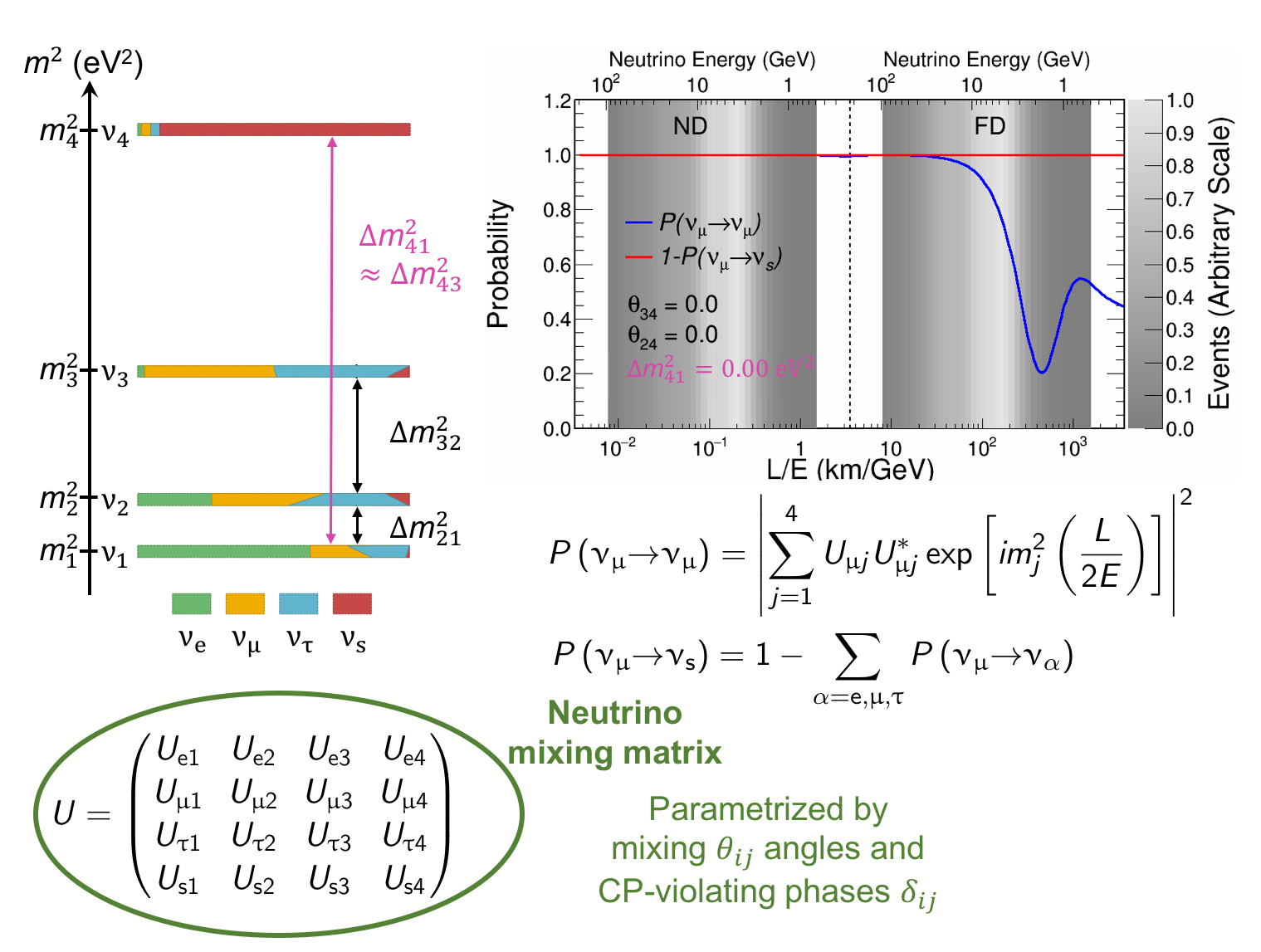
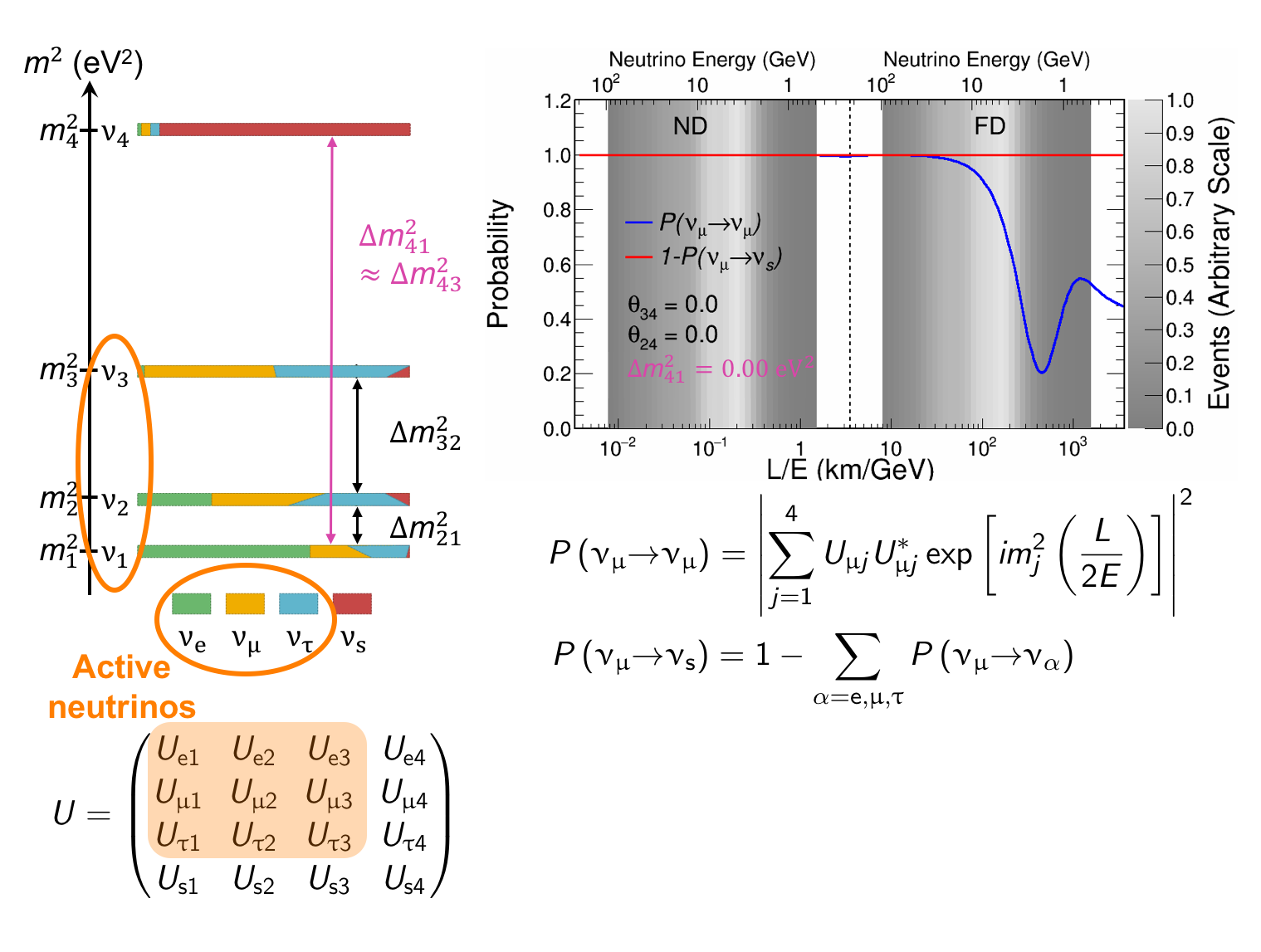
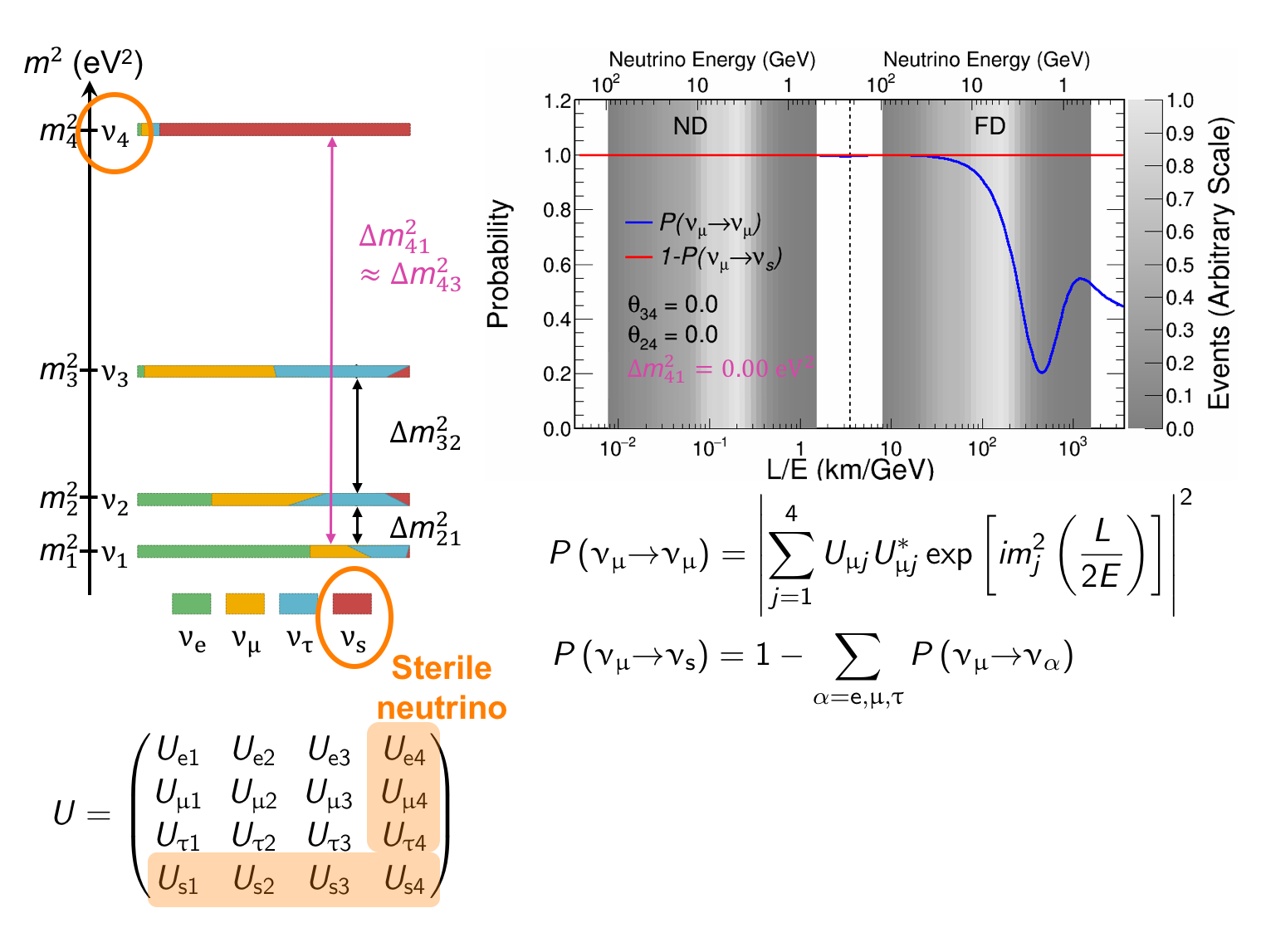
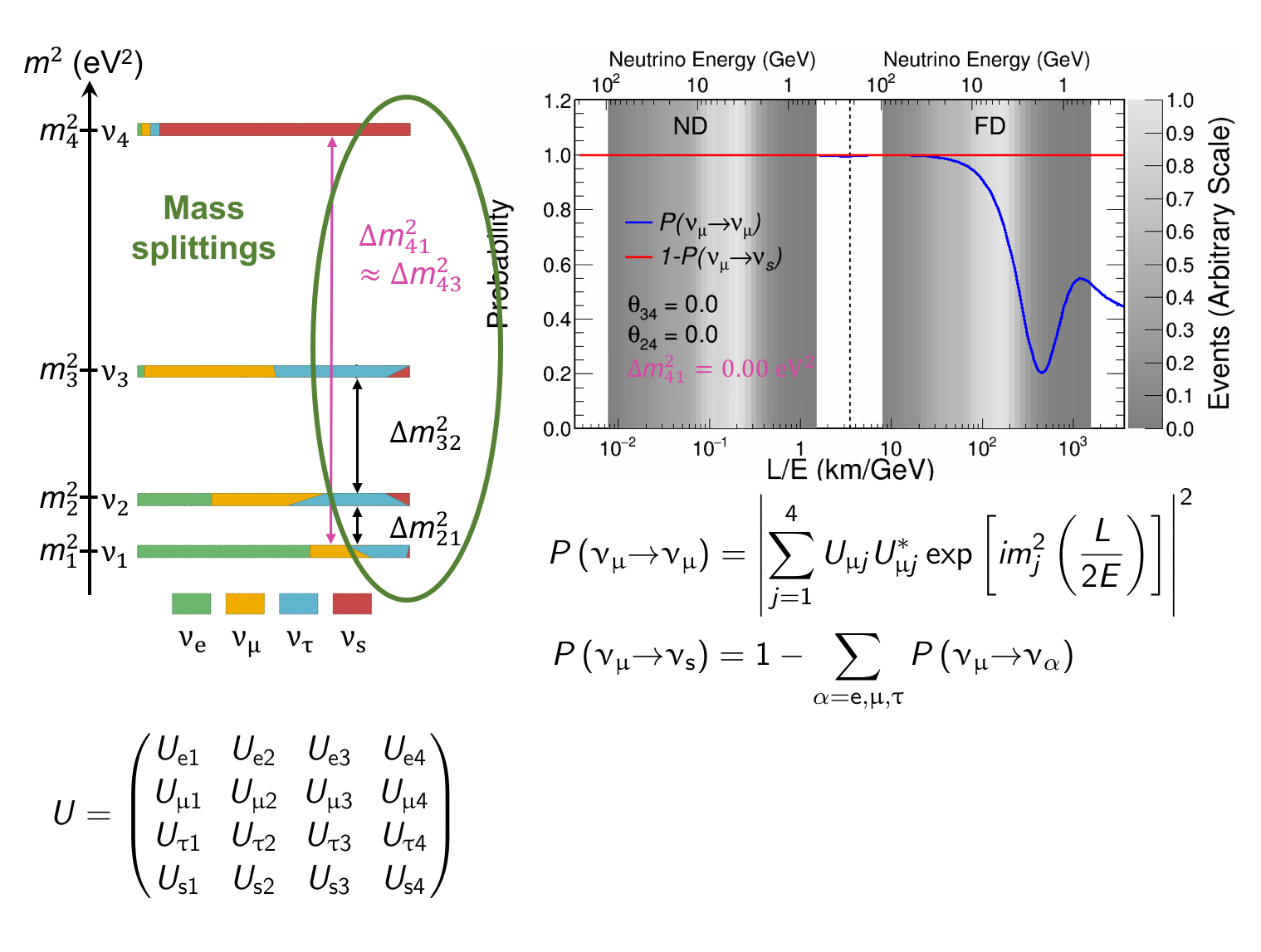
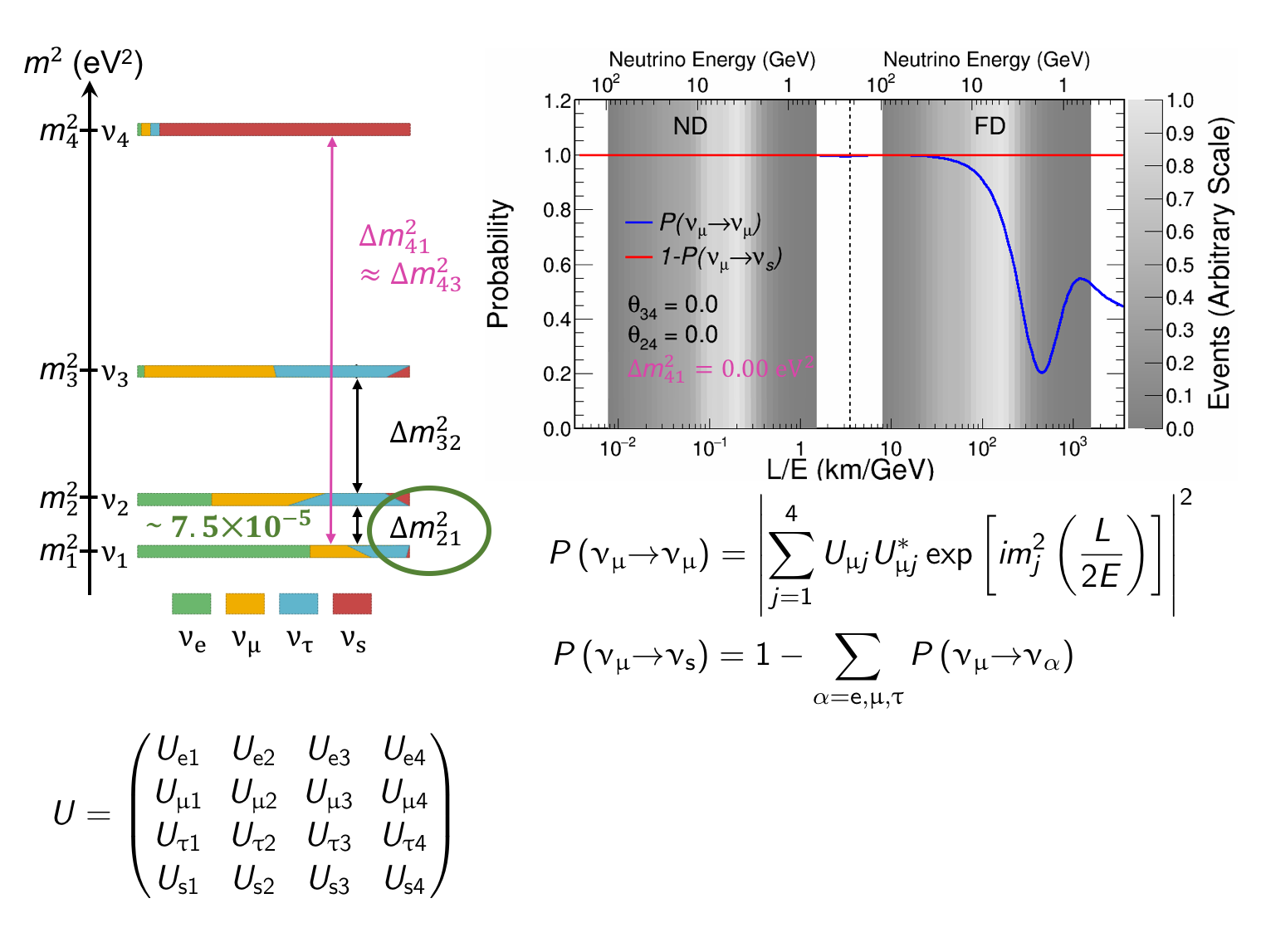
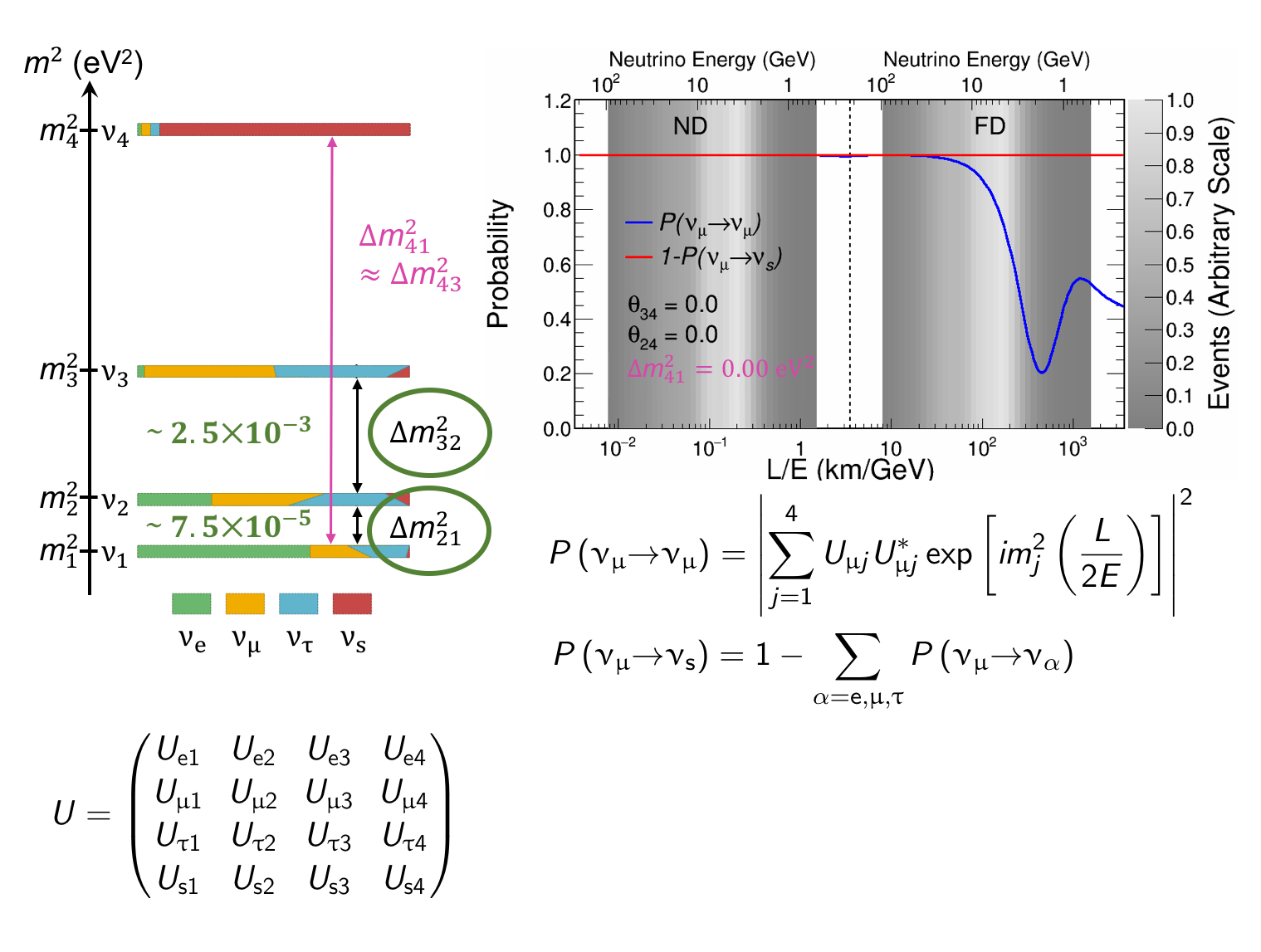
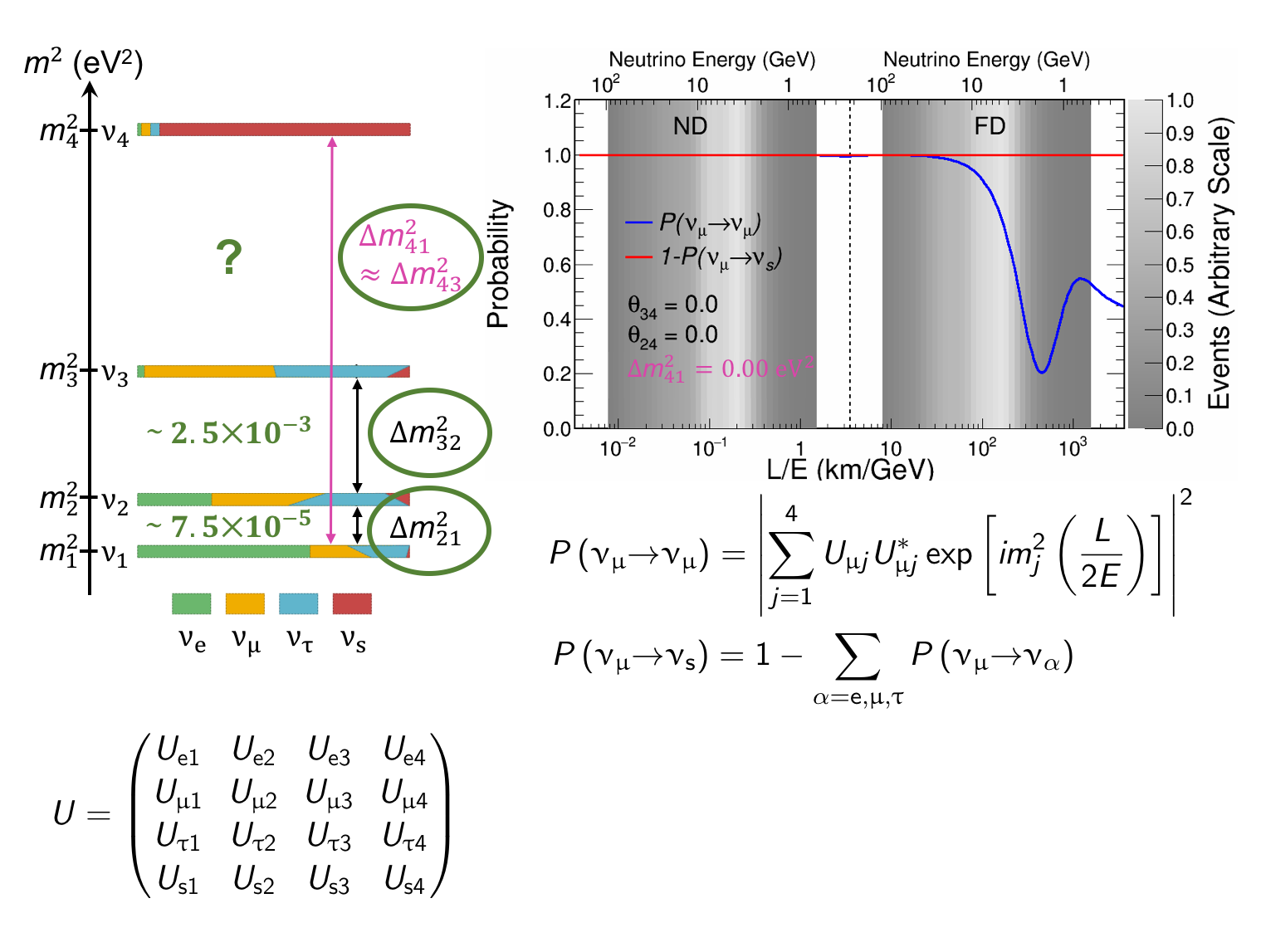
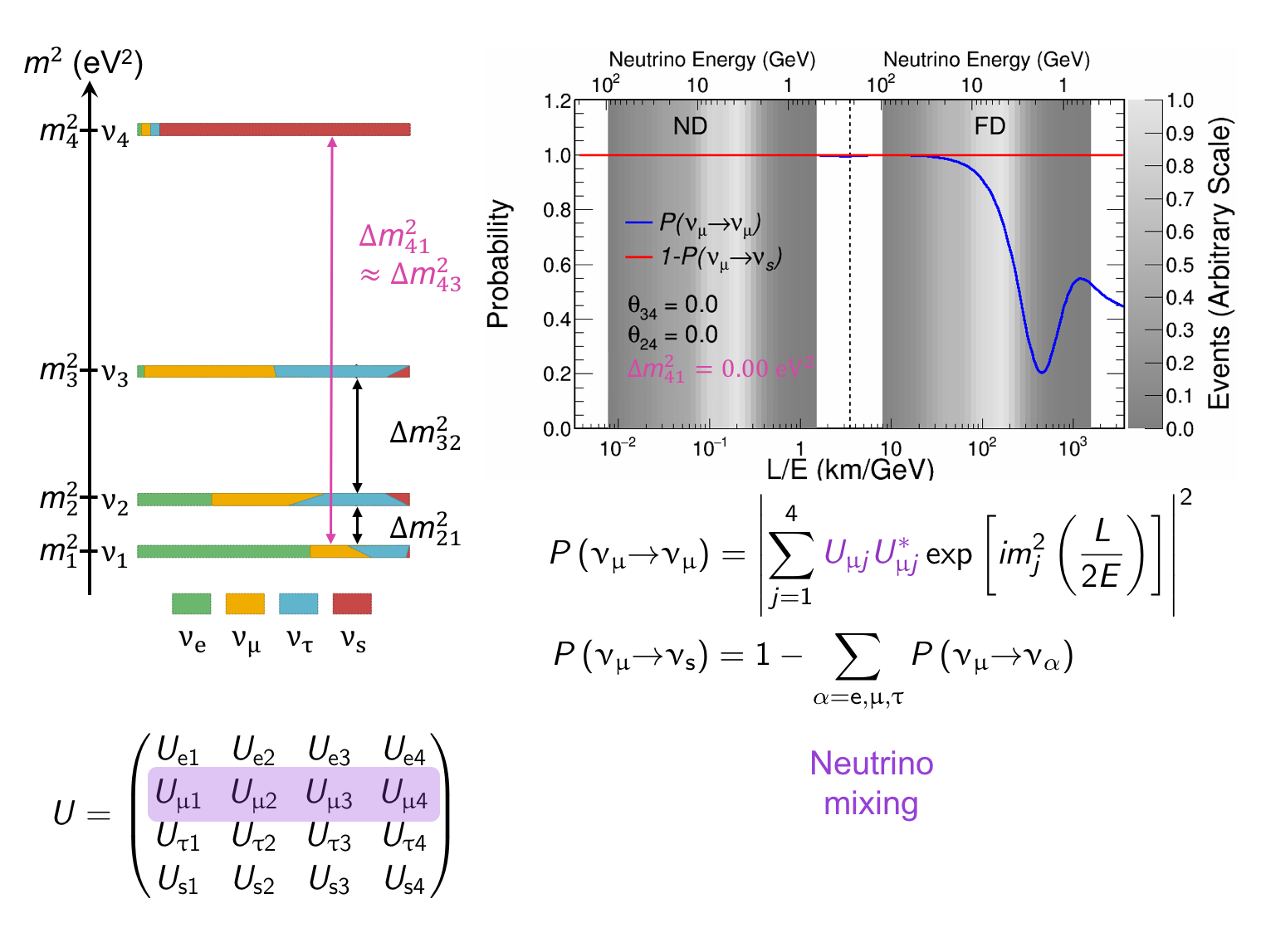
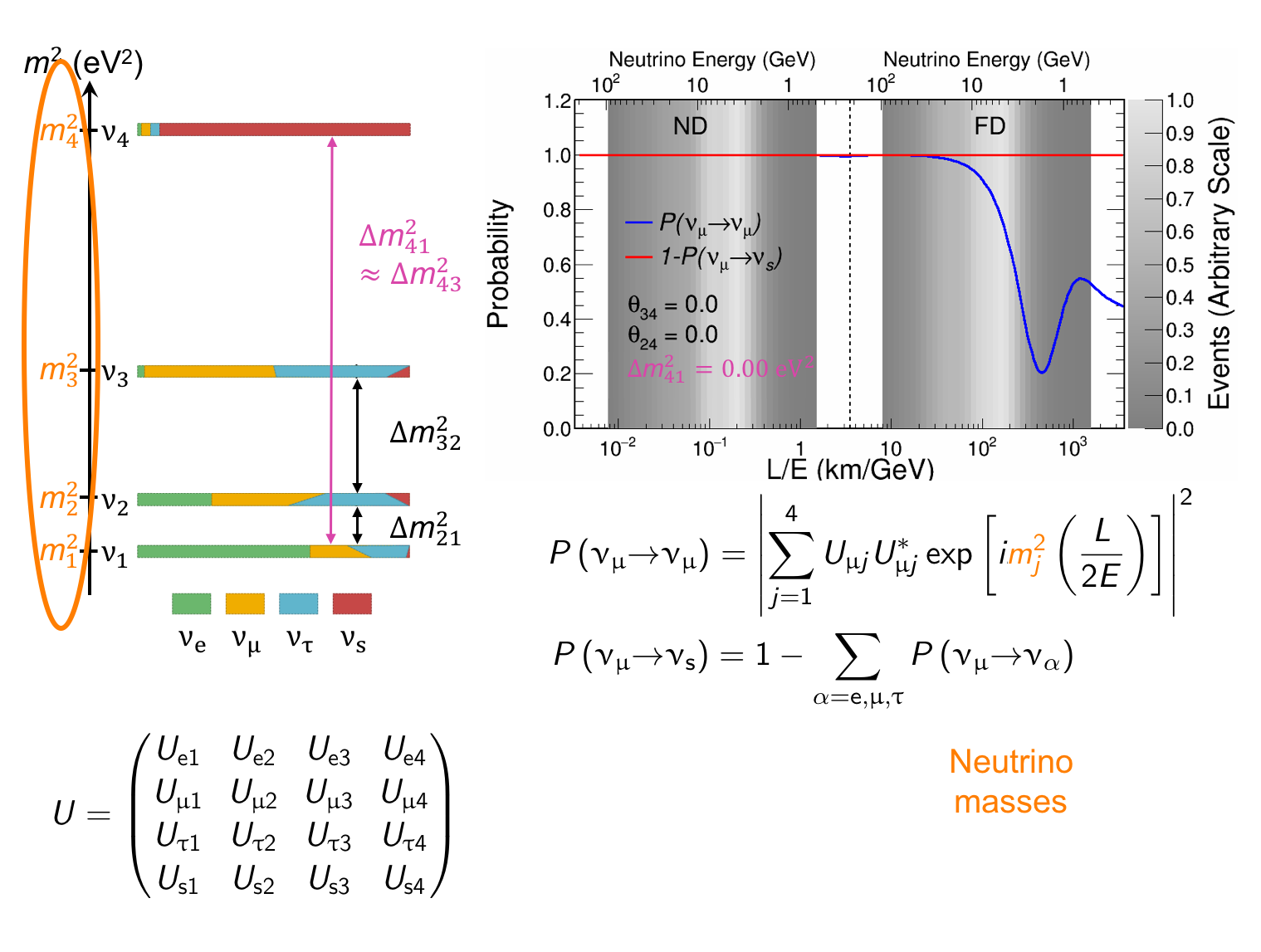
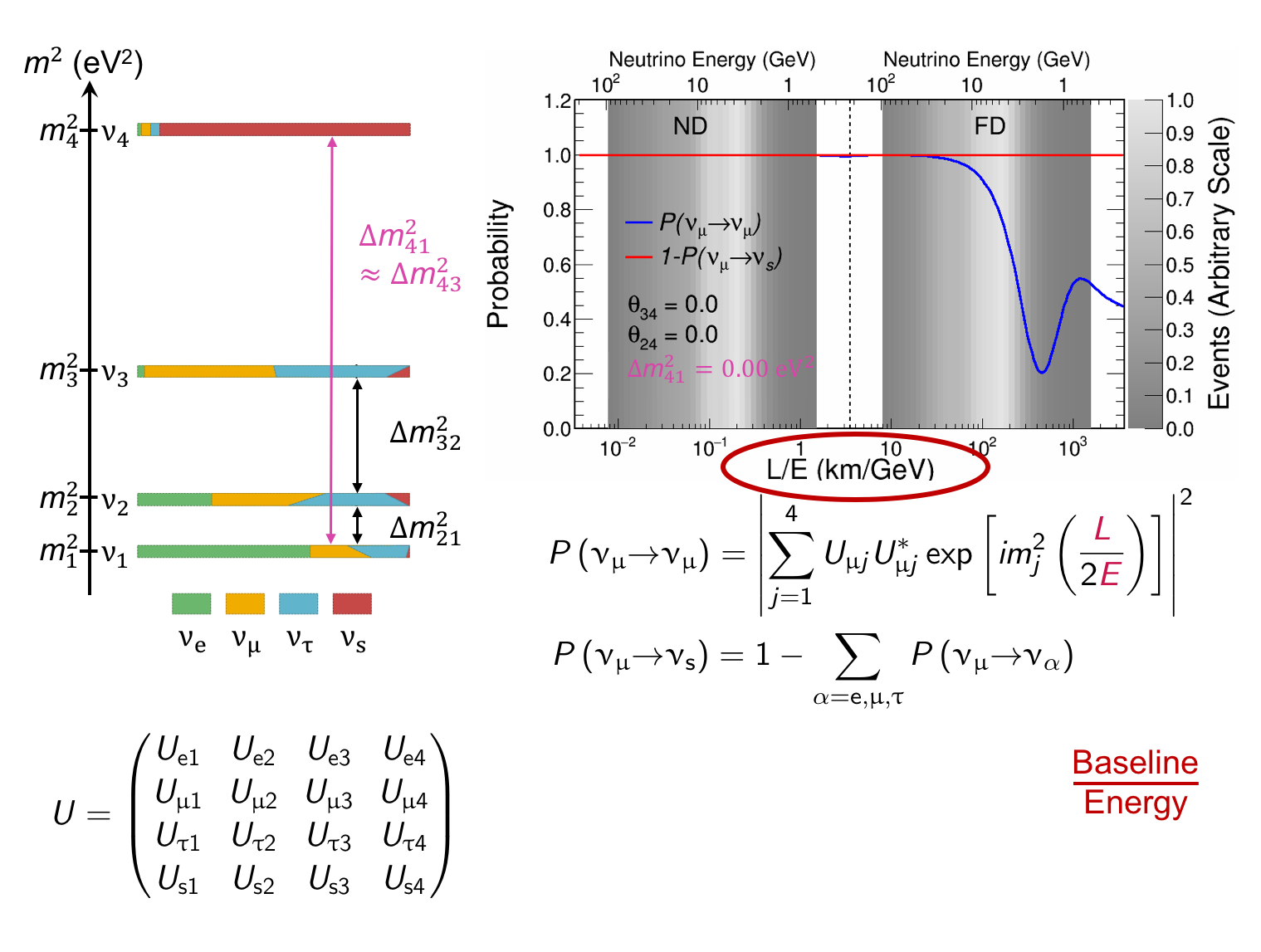
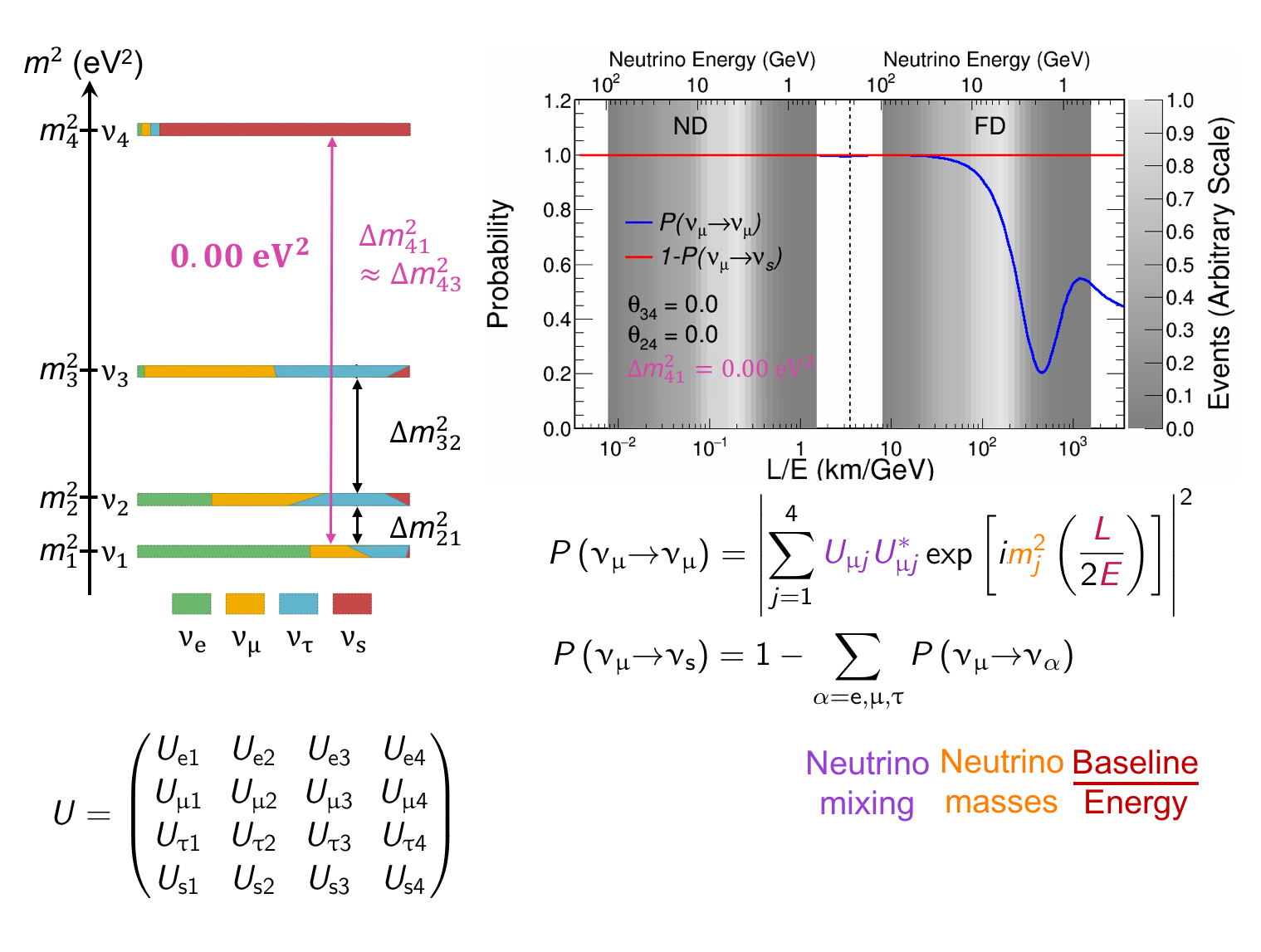
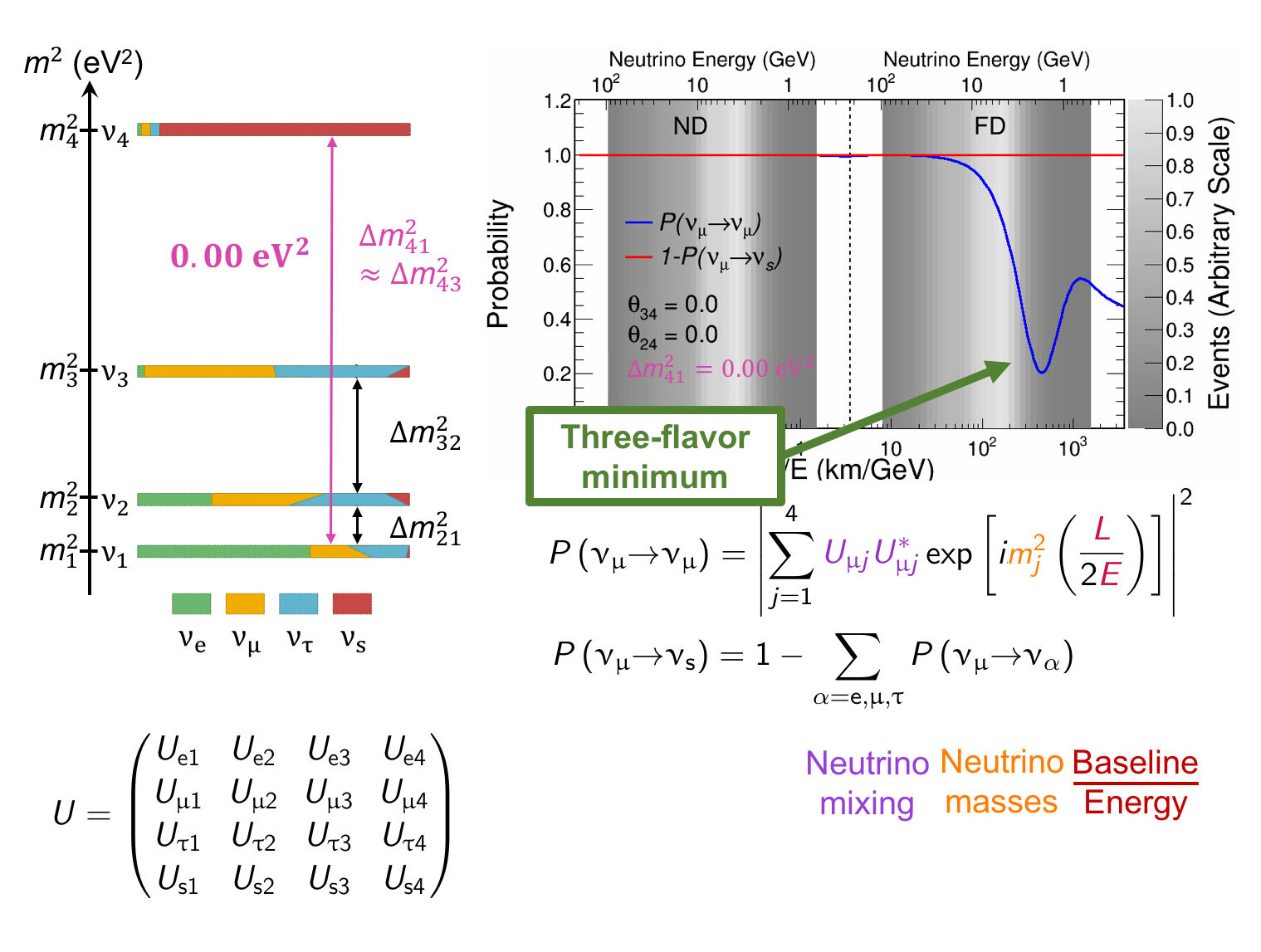
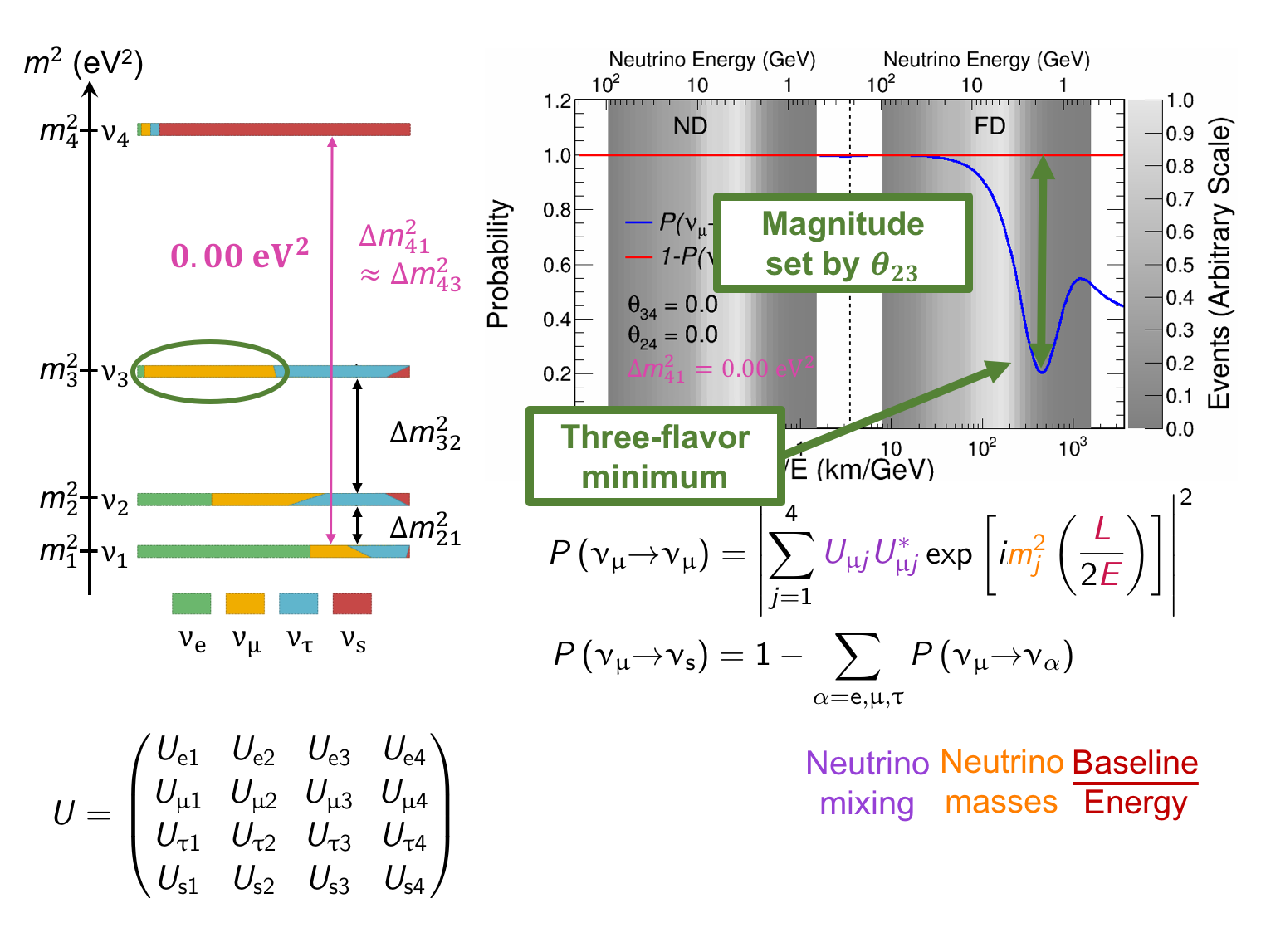
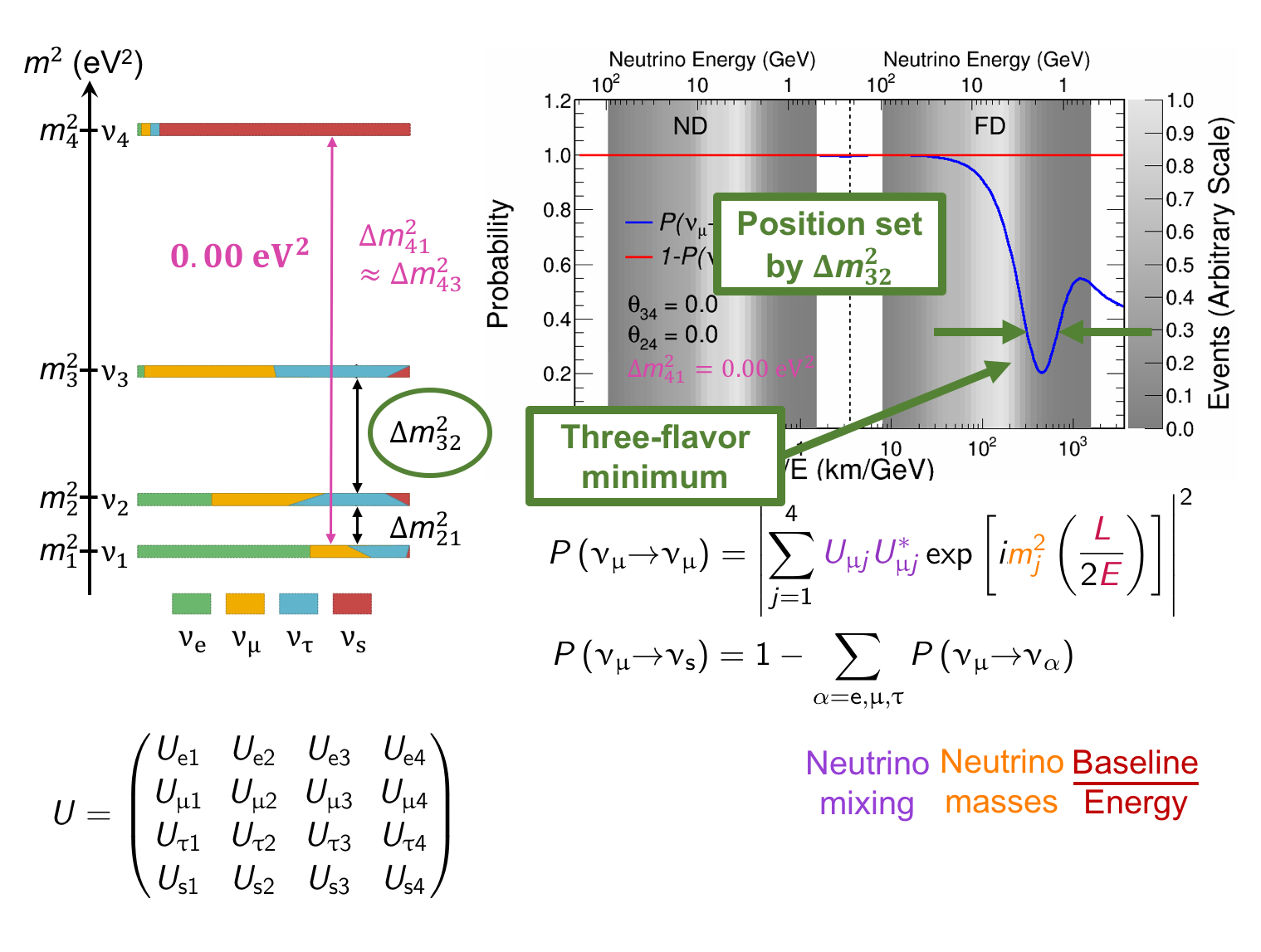
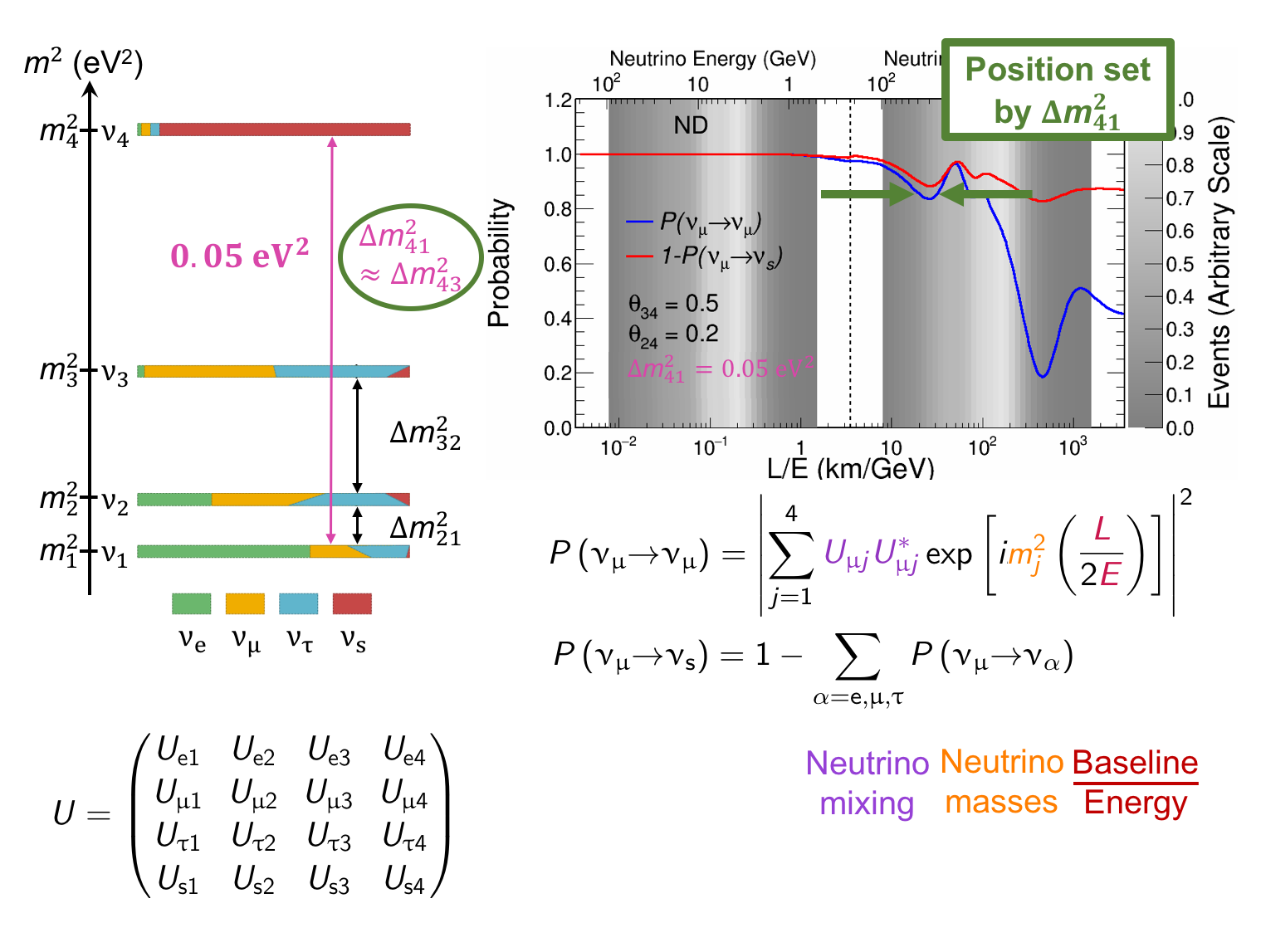
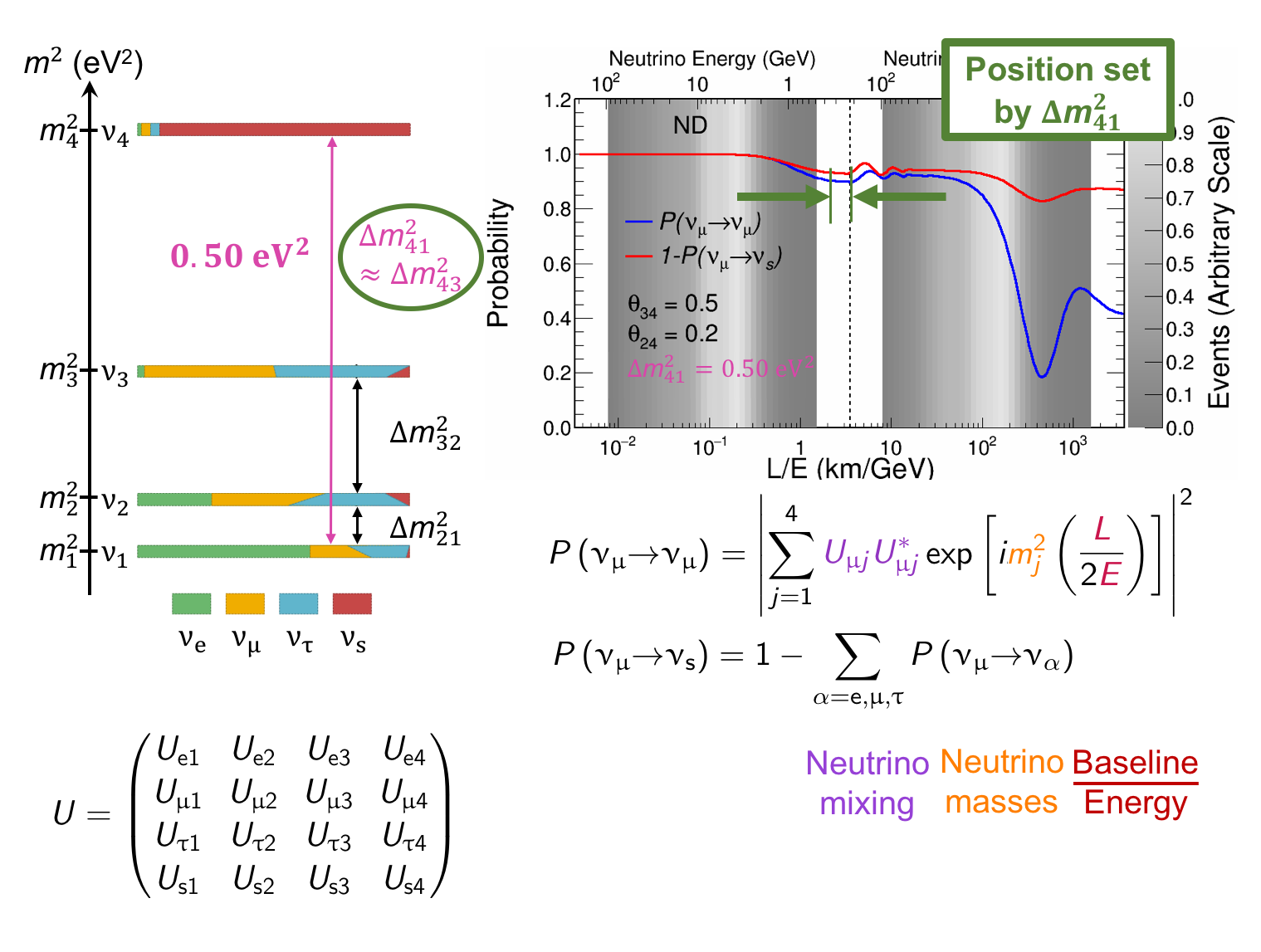
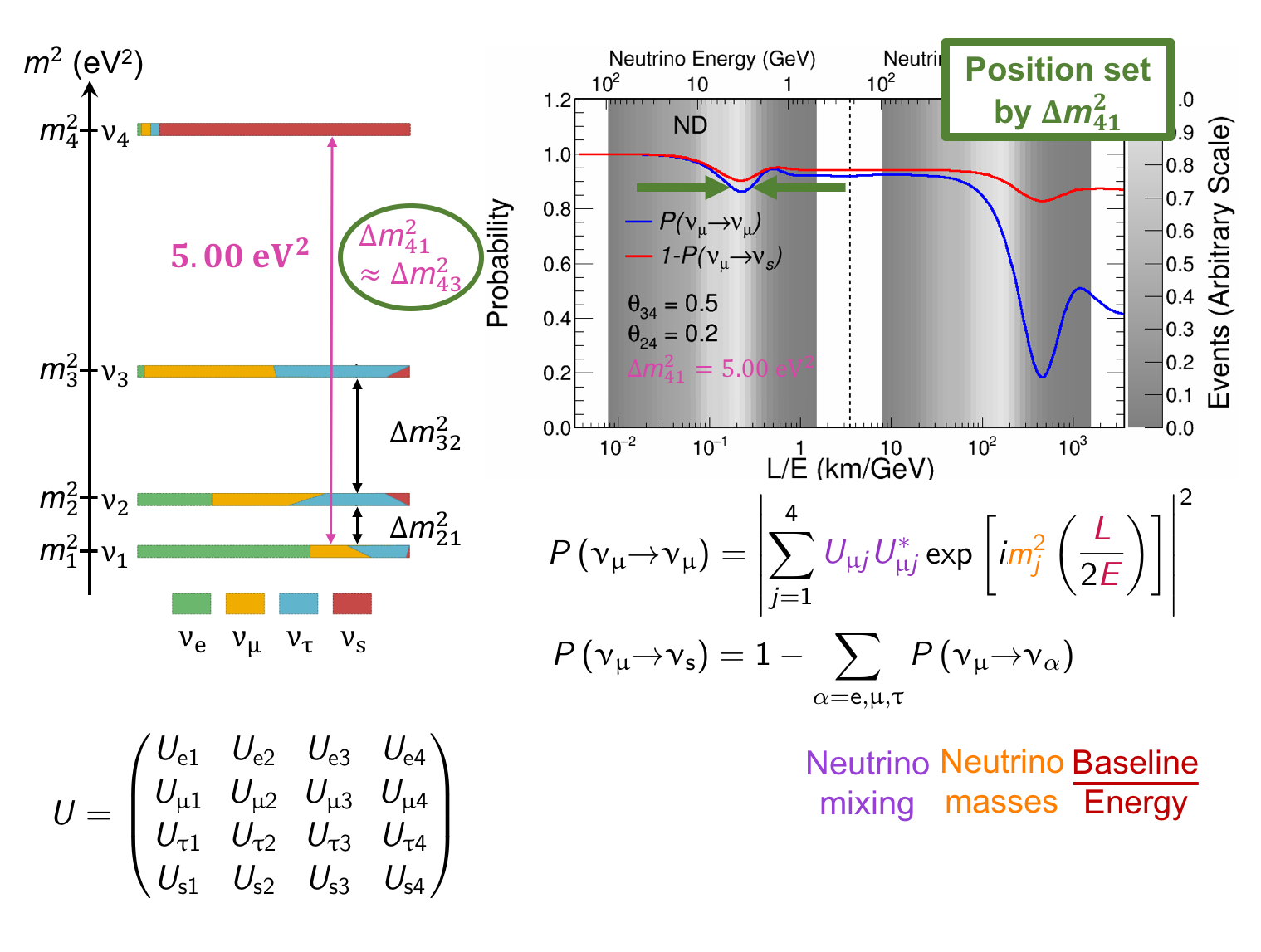
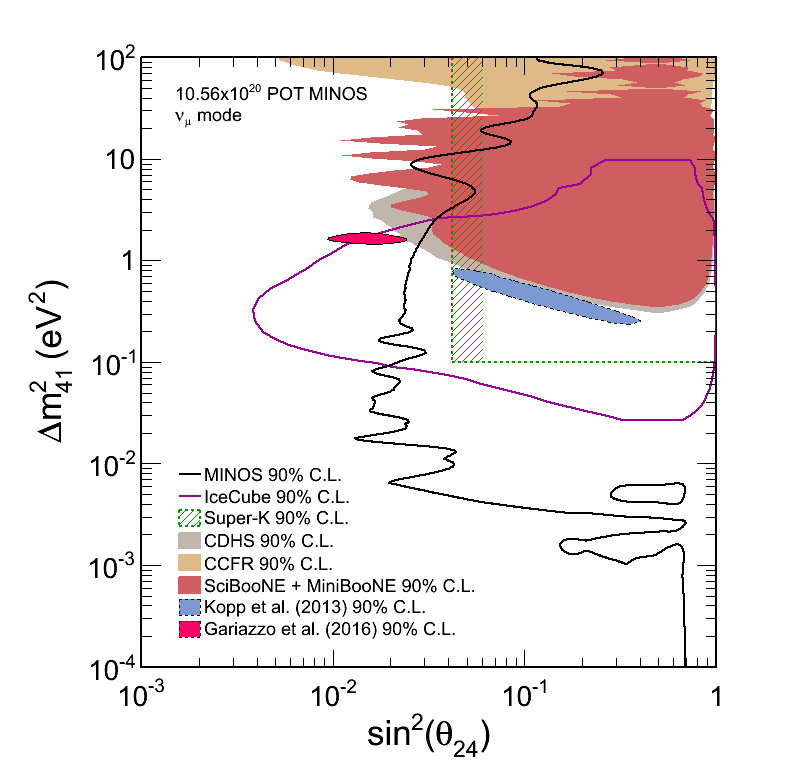
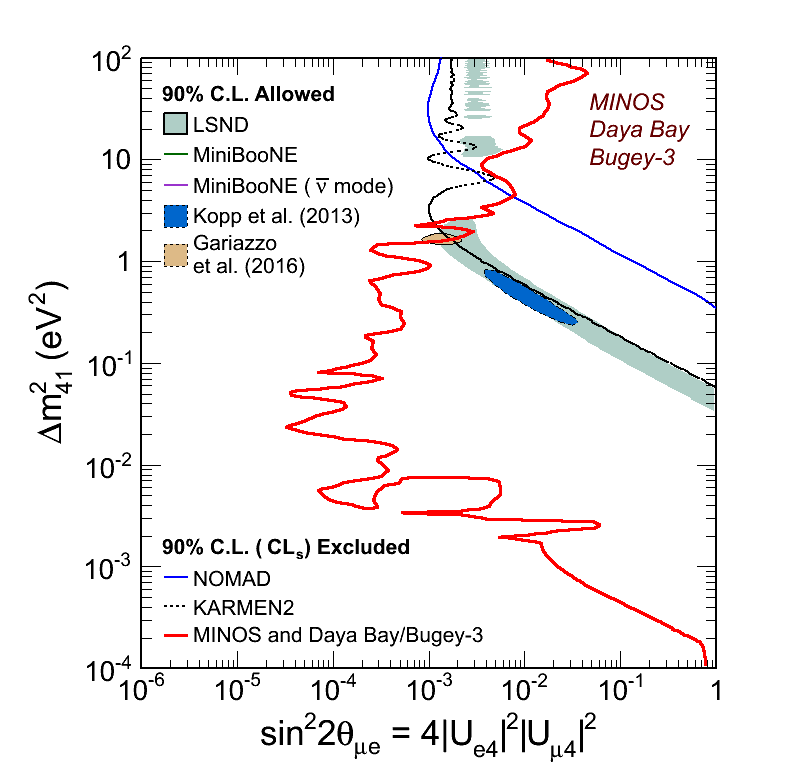
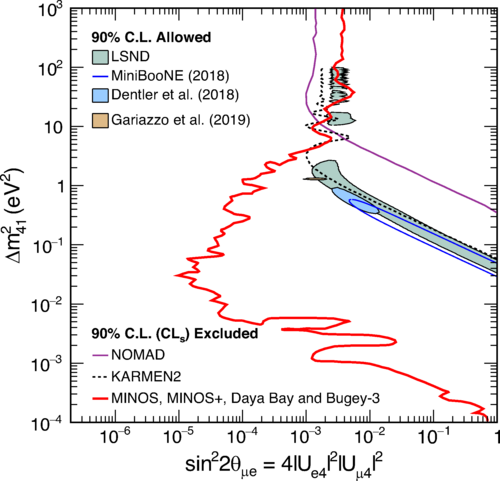
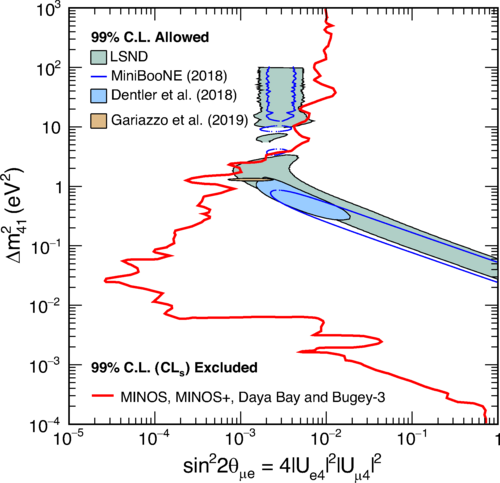
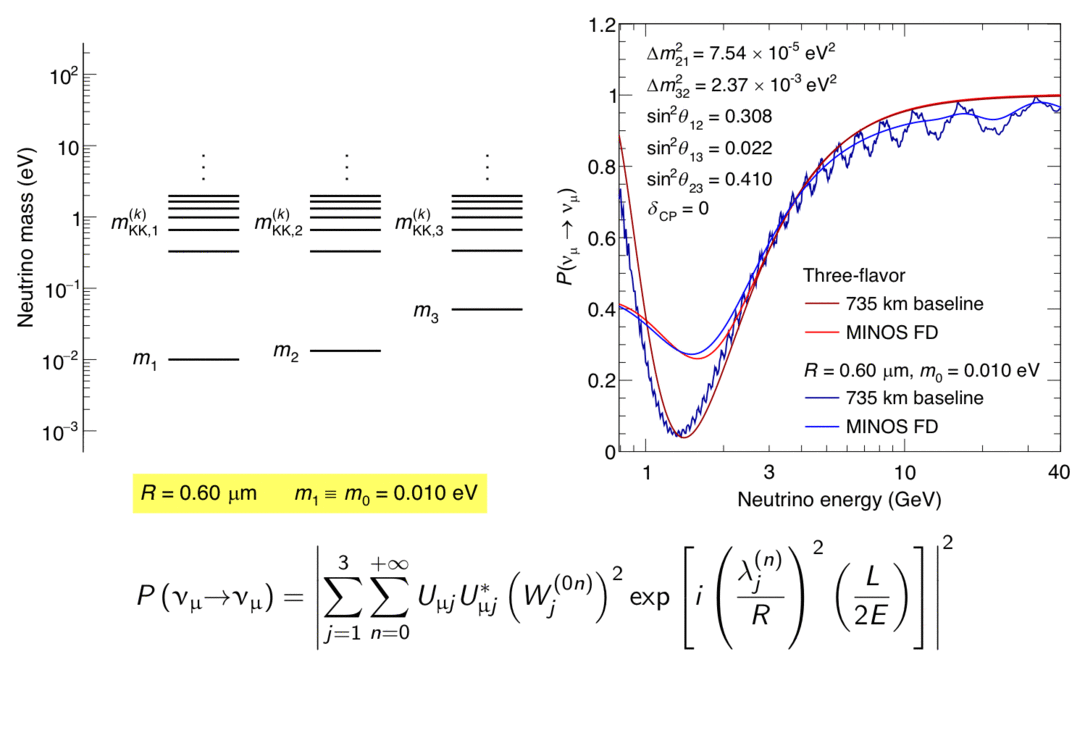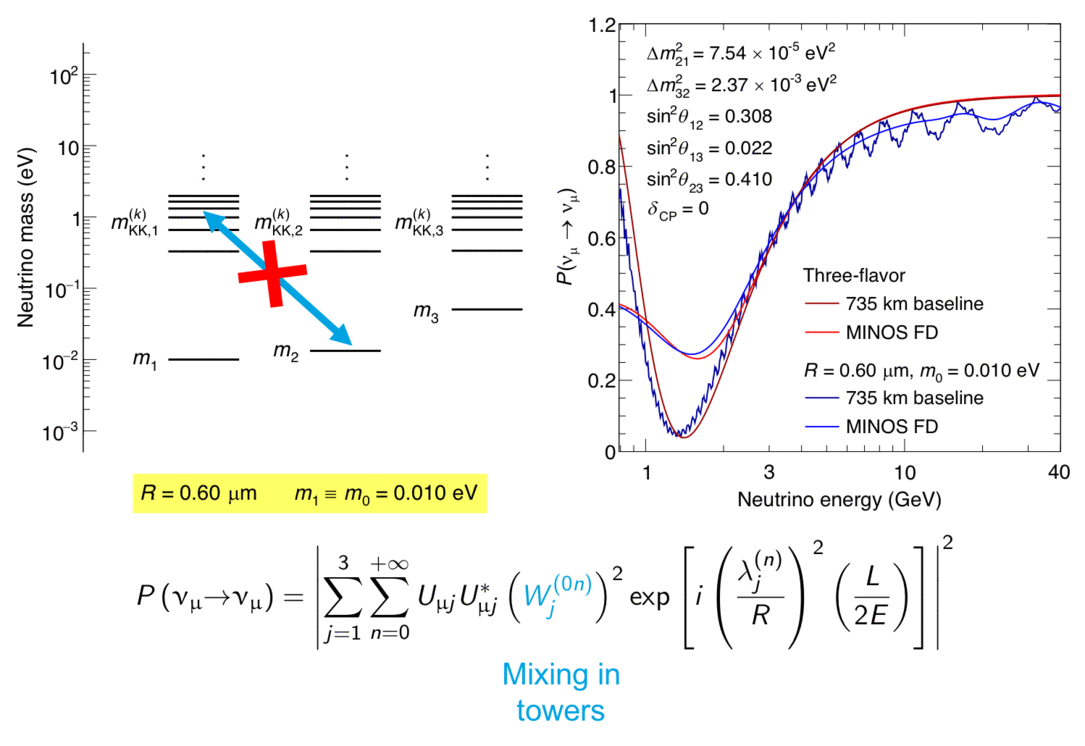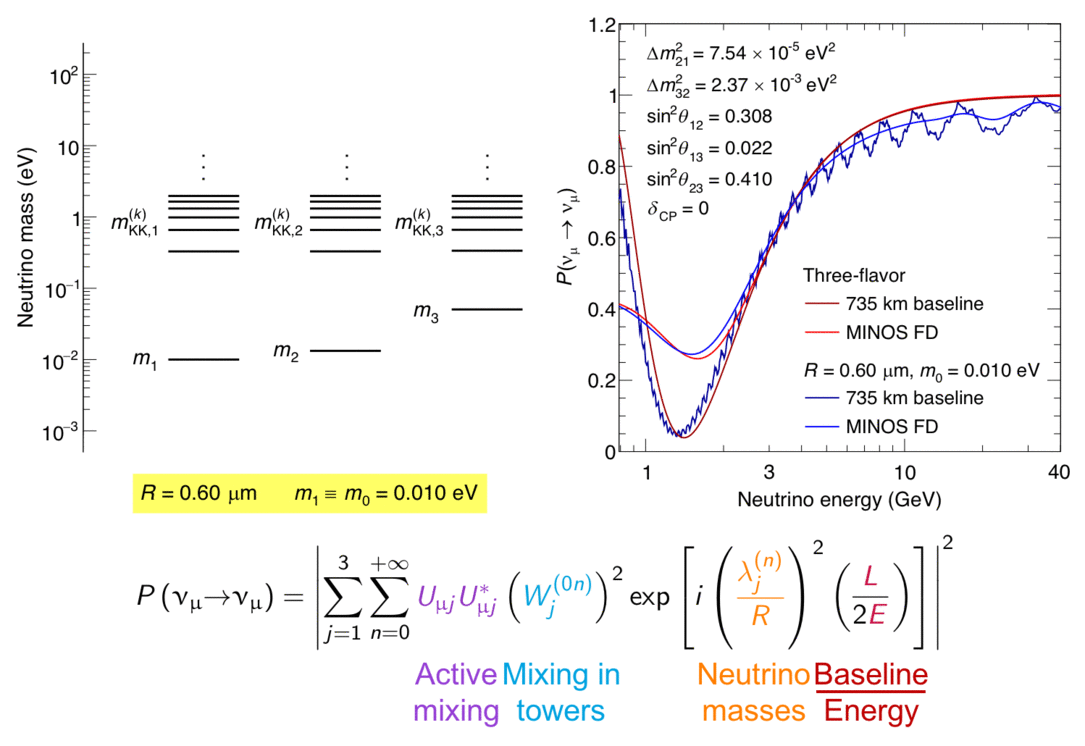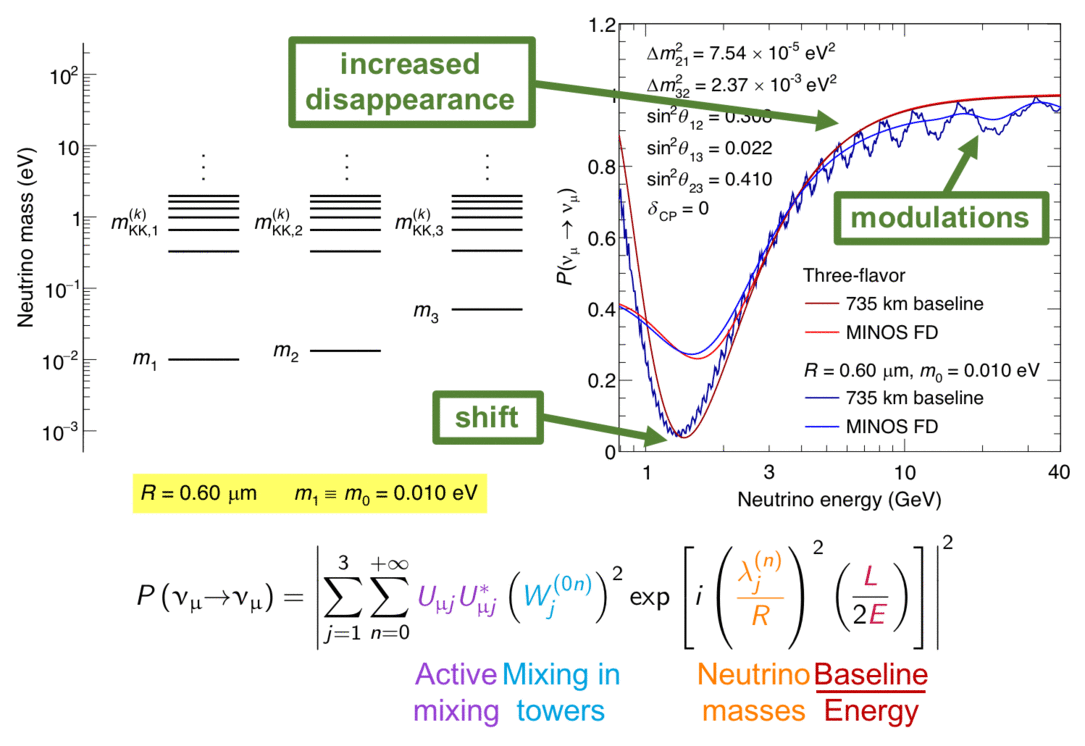
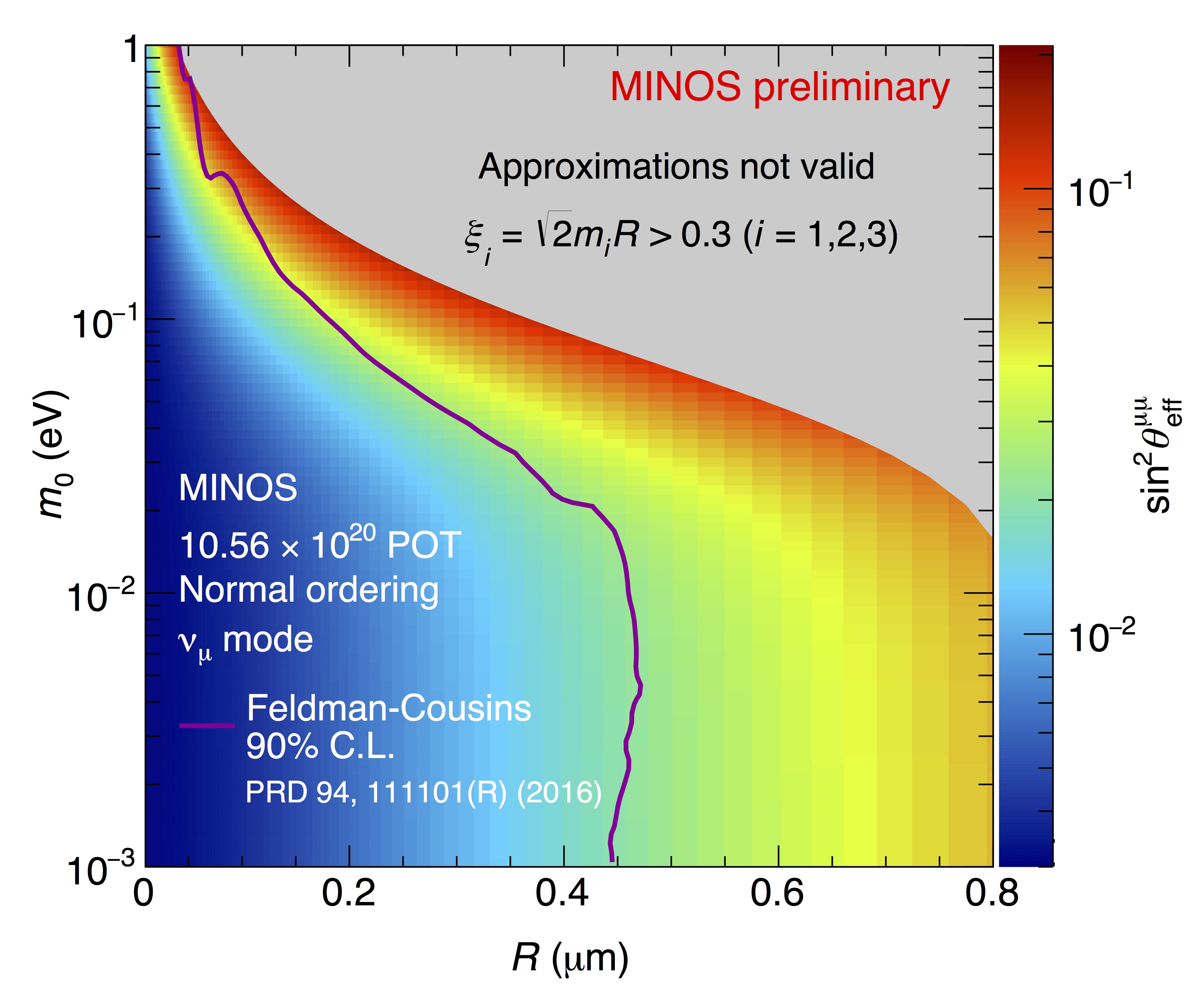
The MINOS experiment was operational between July 2003 and April 2012, detecting neutrinos from the NuMI neutrino beam with a peak neutrino energy of about 3 $~$ GeV. MINOS was continued by MINOS+, which collected data between October 2013 and June 2016, using a NuMI neutrino beam with a peak neutrino energy shifted to about 7 $~$ GeV. This shift to higher energies away from the three-flavor oscillation maximum around 1.5 $~$ GeV increased the sensitivity to neutrino oscillation models beyond the three-flavor paradigm, including sterile neutrinos, large extra dimensions, and non-standard interactions.

The UTKL Research Group has been active on all fronts in the MINOS and MINOS+ Experiments, from detector R $\&$ D, data acquisition, detector calibration, service work, and simulation, to data analysis. Currently we are analyzing the final MINOS+ data.

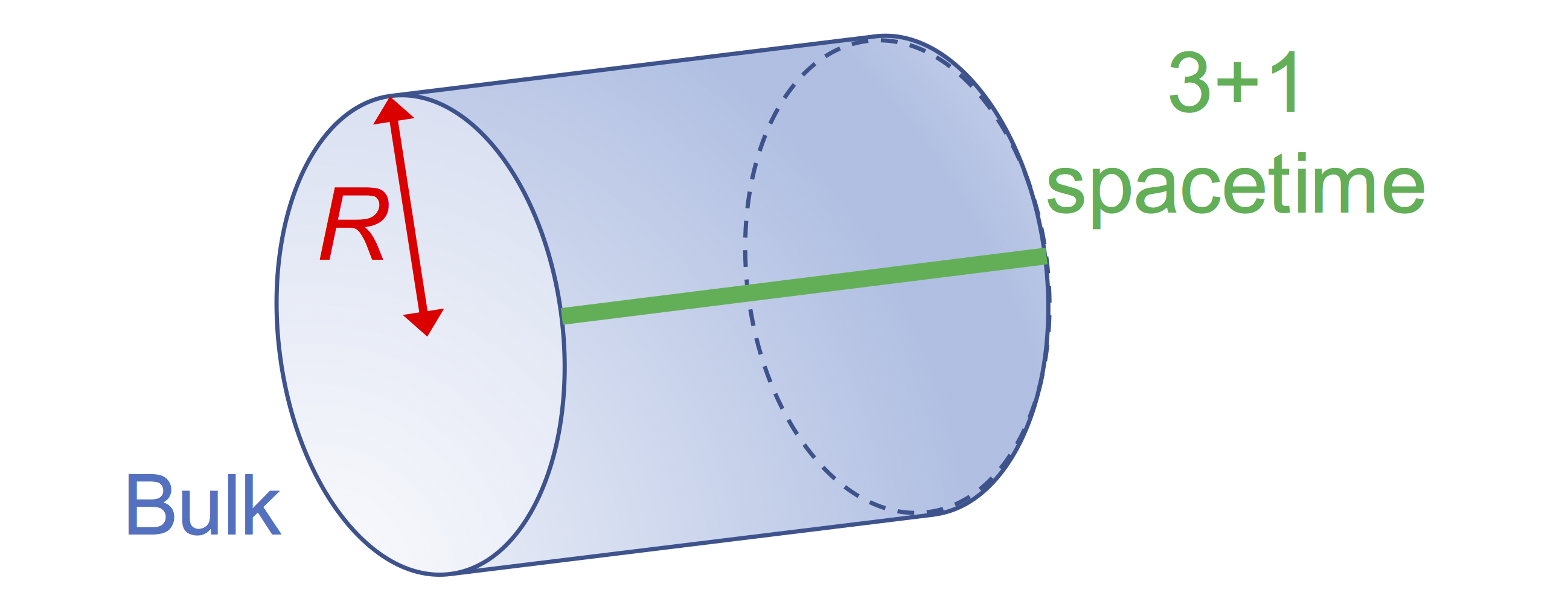
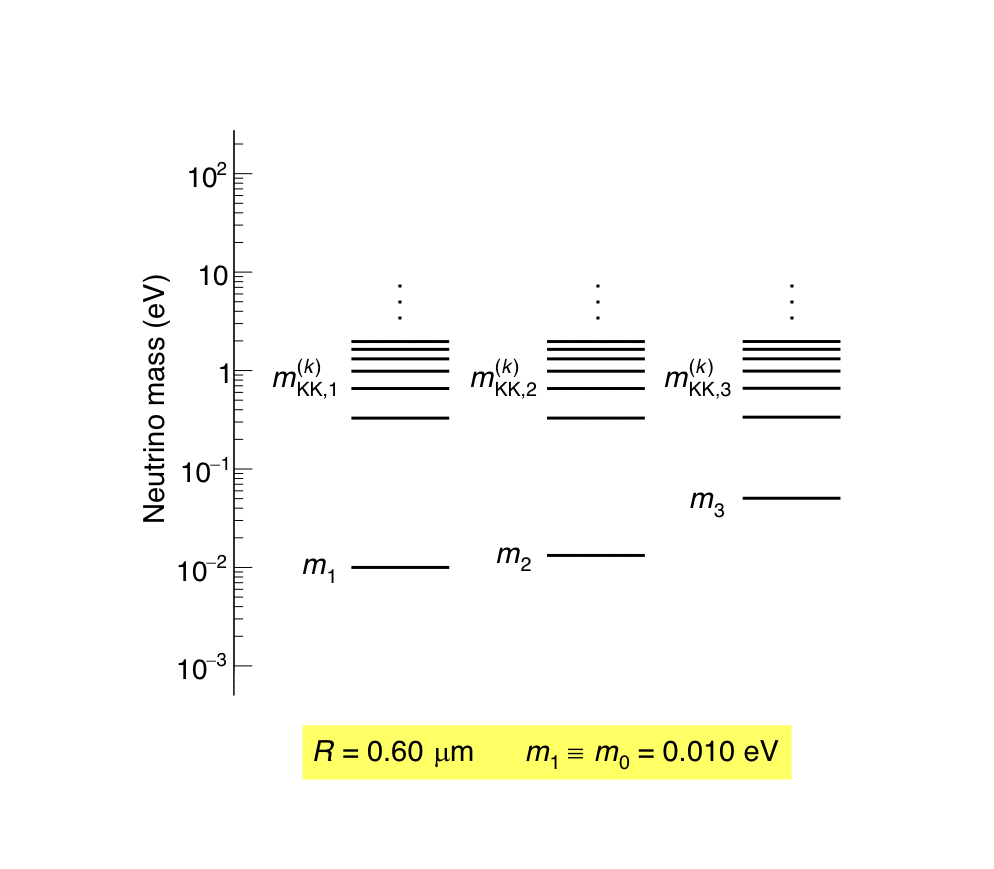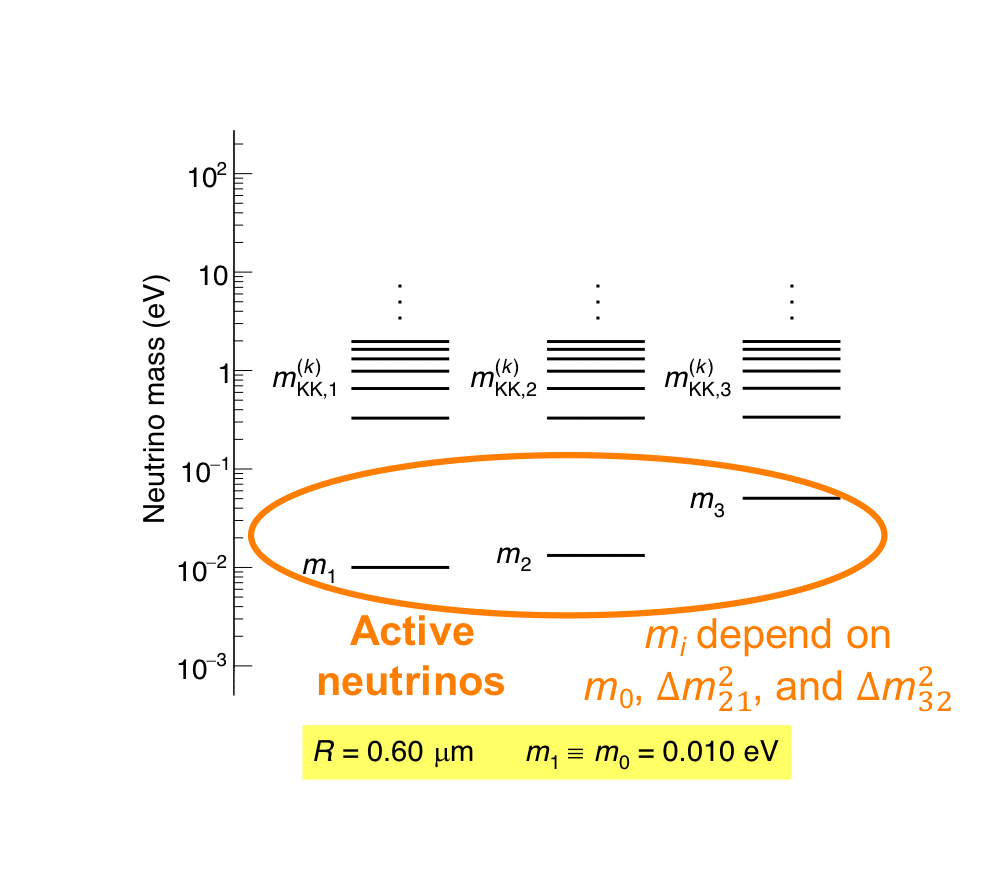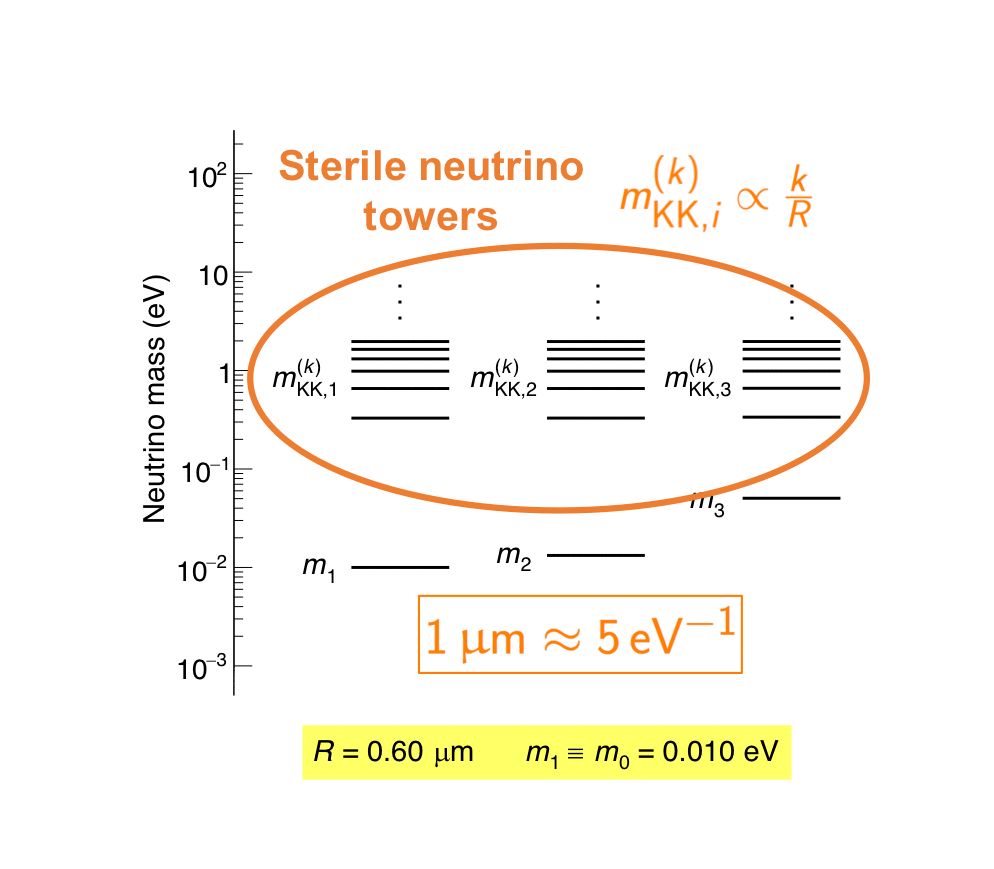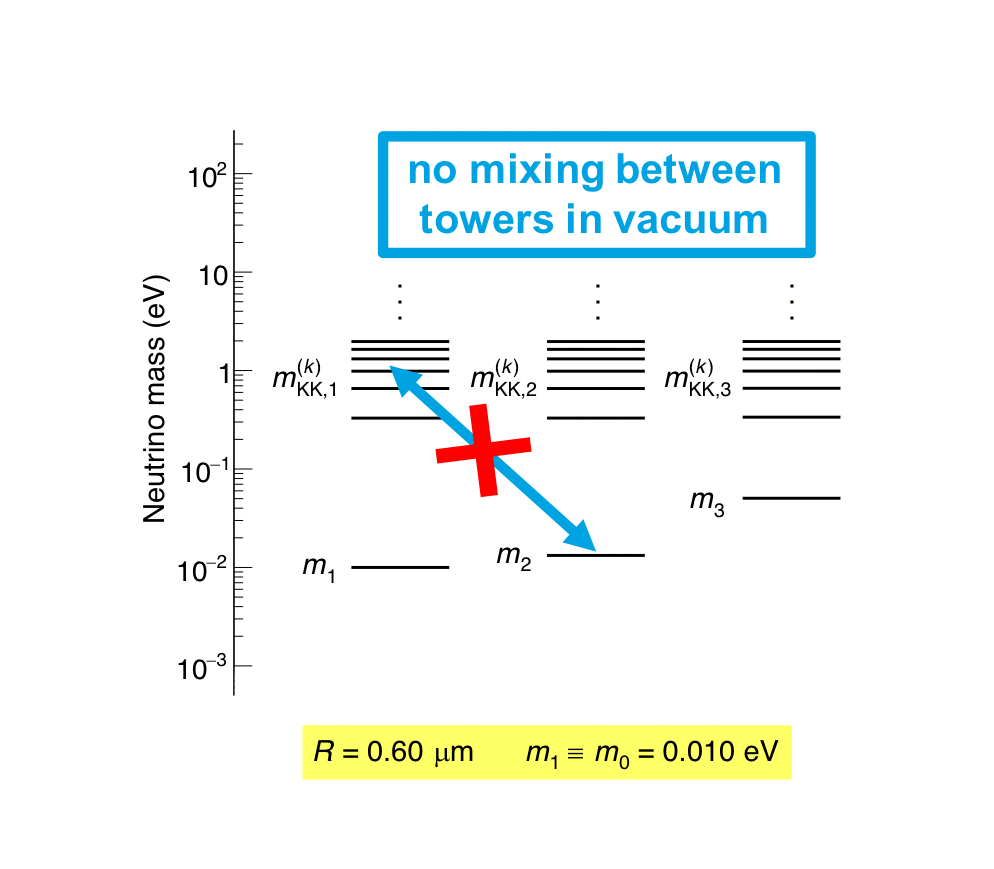
Find out more about the Three-Flavor, Four-Flavor, and Large Extra Dimensions searches in MINOS/MINOS+ below or visit the MINOS website.

Three-Flavor Oscillations

The mixing of three neutrino states is experimentally well established by many experiments, including MINOS and MINOS+. This mixing is described by the $3 \times 3$ Pontecorvo-Maki-Nakagawa-Sakata (PMNS) matrix which can be parameterized by three mixing angles $\theta_{12}$ , $\theta_{23}$ , $\theta_{13}$ , and a CP violating phase $\delta$ . The oscillation probabilities can be expressed such that they additionally depend on two mass-splittings $\Delta m^2_{21}$ and $\Delta m^2_{32}$ where $\Delta m^2_{ij} = m^2_i - m^2_j$ , see Fig 1. MINOS and MINOS+ have made precision measurements (arXiv:2006.15208 [hep-ex]) of the three-flavor atmospheric oscillation parameters $\Delta m^2_{32}$ and $\theta_{23}$ , see Fig 4.

Figure 1: Measuring the atmospheric neutrino oscillation parameters $\Delta m^2_{32}$ and $\theta_{23}$ with MINOS. (Left) In the three-flavor paradigm, the muon neutrino disappearance along the MINOS FD baseline is determined by the mass-splitting $\Delta m^2_{32}$ and the mixing angle $\theta_{23}$ . (Right) The top figure compares the number of muon neutrino events measured by MINOS as a function of neutrino energy (black points) to the number of events predicted by the three-flavor model if there would be no oscillations (grey line) and the number of events predicted by the three-flavor model that agrees best with the MINOS data (red line). The bottom plot takes the ratio of the data and best prediction to the prediction of no oscillations, which is equivalent to the muon neutrino disappearance probability in the FD. The position of the minimum around 1.5 $~$ GeV depends on the magnitude of $\Delta m^2_{32}$ , while the depth of the minimum is approximately set by $\sin^2 \theta_{23}$ .

Figure 2: Top: The reconstructed energy spectra for MINOS and MINOS+ events selected within the Far Detector fiducial volume for data (black points) and the best fit MC predictions for MINOS (red hatched histogram), MINOS+ (blue hatched histogram) and the sum (cyan line). The prediction at the FD with no oscillations is shown as the orange line. Bottom: The ratios of the data and the oscillated prediction to the no oscillation prediction for MINOS and MINOS+ combined.

We report the final measurement of the neutrino oscillation parameters $\Delta m_{32}^2$ and $\sin^2\theta_{23}$ using all data from the MINOS and MINOS+ experiments. These data were collected using a total exposure of $23.76 \times 10^{20}$ protons on target producing $\nu_\mu$ and $\bar{\nu}_\mu$ beams and $60.75$ kt $\cdot$ yr exposure to atmospheric neutrinos. The measurement of the disappearance of $\nu_\mu$ and the appearance of $\nu_e$ events between the Near and Far detectors yields $|\Delta m_{32}^2| = 2.40^{+0.08}_{−0.09}~(2.45^{+0.07}_{−0.08})\times10^{-3}\,\text{eV}^2$ and $\sin^2 \theta_{23} = 0.43^{+0.20}_{−0.04}~(0.42^{+0.07}_{−0.03})$ at $68\%$ C.L. for Normal (Inverted) Hierarchy.

Figure 3: 1D likelihood profiles as functions of $\Delta m_{32}^2$ and $\sin^2 \theta_{23}$ for each hierarchy.

Figure 4: The $90\%$ confidence limits on $\Delta m_{32}^2$ and $\sin^2 \theta_{23}$ for the normal mass hierarchy, comparing MINOS+, IceCube [PhysRevLett.120.071801], NOvA [PhysRevLett.123.151803], Super-K [PhysRevD.97.072001], and T2K [Nature 580, 339–344(2020)].

Four-Flavor Oscillations

Neutrino oscillations between three neutrino flavors (electron, muon, and tau) are experimentally well established through measurements of solar, atmospheric, nuclear reactor, and accelerator beam neutrinos [Chin. Phys. C 38, 090001 (2014)] and are consistent with LEP results constraining the number of light neutrinos to three ( $m_{\nu} < \frac{1}{2}m_{\text{Z}} \approx 45\,\text{GeV}$ ) through measurements of the invisible part of the $Z$ boson decay width [J.PhysRep.2005.12.006]. The three-flavor paradigm is discussed in more detail in Three-Flavor Oscillations. There are, however, hints for the existence of an additional neutrino flavor. These include the anomalous electron antineutrino appearance in short-baseline muon antineutrino beams at LSND [PhysRevD.64.112007] and MiniBooNE [PhysRevLett.110.161801], which require a fourth neutrino state corresponding to a mass-splitting scale of about 1 eV $^2$ . Given the LEP measurements, such a neutrino state would not couple through the Standard Model interactions and as such is called a sterile neutrino.

Mixing between the three active neutrinos and the sterile neutrino modifies the three-flavor oscillation probabilities, as illustrated in Fig. 1. The $3\times3$ matrix describing mixing in the three-flavor paradigm can be extended to a $4\times4$ matrix to accommodate the fourth neutrino state, as illustrated in Fig. 1. This introduces three additional mixing angles, $\theta_{14}$ , $\theta_{24}$ , and $\theta_{34}$ , as well as two additional charge-parity (CP) violating phases, $\delta_{14}$ and $\delta_{24}$ . Furthermore, three new mass-splittings, $\Delta m^2_{41}$ , $\Delta m^2_{42}$ and $\Delta m^2_{43}$ , enter the oscillation probabilities.

Figure 1: (Left) Mass-splitting structure in the four-flavor scenario and the four-flavor mixing matrix. (Right) Effect of the mass-splitting $\Delta m^2_{41}$ on the four-flavor oscillation probabilities.

MINOS and MINOS+ are sensitive to $\Delta m^2_{41}$ , $\theta_{24}$ , and $\theta_{34}$ through muon neutrino disappearance. MINOS reported [PhysRevLett.117.151803] strong constraints on $\sin^2 \theta_{24}$ over a wide range of $\Delta m^2_{41}$ values, as shown in Fig. 2. A collaboration with the Daya-Bay reactor neutrino experiment [PhysRevLett.117.151801], which is sensitive to $\Delta m^2_{41}$ and $\theta_{24}$ through long-baseline electron antineutrino disappearance, allows to constrain the four-flavor model in terms of $\Delta m^2_{41}$ and $\sin^2 \theta_{\mu\text{e}} = 4 \vert U_{\text{e}4} \vert^2 \vert U_{\mu4} \vert^2$ , as shown in Fig. 2. This result can be directly compared to the LSND and MiniBooNE results.

Figure 2: The MINOS data 90 $\%$ Feldman-Cousins corrected C.L. obtained using muon neutrino disappearance and searching for a deficit in NC events. The MINOS coverage is compared to other experimental results and to two global fits. (Right) The MINOS and Daya Bay/Bugey-3 combined 90 $\%$ C.L. $_{\rm{S}}$ limit on $\sin^{2}2\theta_{\mu e}$ compared to the LSND and MiniBooNE 90 $\%$ C.L. allowed regions.

Recently, the combination of MINOS/MINOS+, Bugey-3 and Daya-Bay has been updated [PhysRevLett.125.071801] with new results from the Daya-Bay and MINOS+ experiments. Significantly improved constraints on the $\theta_{\mu e}$ mixing angle are derived that constitute the most constraining limits to date over five orders of magnitude in the mass-squared splitting $\Delta m_{41}^2$ , excluding the $90\%$ C.L. sterile-neutrino parameter space allowed by the LSND and MiniBooNE observations at $90\%$ CLs for $\Delta m_{41}^2 < 13\,\text{eV}^2$ . Furthermore, the LSND and MiniBooNE $99\%$ C.L. allowed regions are excluded at $99\%$ CLs for $\Delta m_{41}^2 < 1.6\,\text{eV}^2$ . See below.

Figure 3: (Left) Comparison of the MINOS, MINOS+, Daya Bay, and Bugey-3 combined $90\%$ CLs limit on $\sin^2 2\theta_{\mu e}$ to the LSND and MiniBooNE $90\%$ C.L. allowed regions. Regions of parameter space to the right of the red contour are excluded. (Right) Comparison of the MINOS, MINOS+, Daya Bay, and Bugey-3 combined $99\%$ CLs limit on $\sin^2 2\theta_{\mu e}$ to the LSND and MiniBooNE $99\%$ C.L. allowed regions. The limit also excludes the $99\%$ C.L. region allowed by a fit to global data by Gariazzo et al. where MINOS, MINOS+, Daya Bay, and Bugey-3 are not included [JHEP06(2017)135, J.PhysLetB.2018.04.057], and the $99\%$ C.L. region allowed by a fit to all available appearance data by Dentler et al. [JHEP08(2018)010] updated with the 2018 MiniBooNE appearance results [PhysRevLett.121.221801].

Large Extra Dimensions

Current data are well described by the three-flavor model, as discussed in more detail in Three-Flavor Oscillations and Four-Flavor Oscillations. However, with increasing precision of experiments, one can test for discrepancies that could be accounted for by small modifications to the standard three-flavor model. One such scenario employs large extra dimensions, which in the context of neutrino oscillations also includes sterile neutrinos, but an infinite amount of them.

Figure 1: (Left) Simplified picture of the circular extra dimension in the LED model. (Right) The Kaluza-Klein towers of active and sterile neutrinos for the LED scenario corresponding to an extra dimension radius $R=0.60~\mu$ m and a smallest active neutrino mass $m_0 = 0.010\,$ eV.

In the Large Extra Dimension (LED) model of [5, 6, 7, 8, 9] three SM singlet fermion fields are introduced in an extra dimension with radius $R$ . The extra dimension together with the 3+1 spacetime, or brane, forms the bulk. A simplified picture of the circular extra dimension is given in Fig. 1. The compactness of the extra dimension allows a decomposition of each bulk fermion in Fourier modes, which are interpreted in the brane as Kaluza-Klein (KK) states or infinite towers of neutrinos. The zero modes are identified as the active neutrinos, while the other modes are sterile neutrinos. The Yukawa coupling between the bulk fermions and the active neutrinos leads to mixing between the active and sterile neutrinos, which alters the three-flavor oscillation probabilities, as illustrated in Fig. 2 for muon neutrino disappearance along the MINOS FD baseline. Hence, neutrino oscillation measurements can constrain the size of large extra dimensions. Compared to the three-flavor paradigm, this model requires two extra parameters, $R$ and $m_0$ , where the latter is defined as the lightest active neutrino mass. For normal mass ordering this implies that $m_3 > m_2 > m_1 \equiv m_0$ , while for inverted mass ordering $m_2 > m_1 > m_3 \equiv m_0$ .

Figure 2: The muon neutrino disappearance probability along the MINOS FD baseline (with and without detector resolution effects) for the LED scenario corresponding to an extra dimension radius $R=0.60~\mu$ m and a smallest active neutrino mass $m_0 = 0.010~$ eV.

MINOS recently reported [10] the strongest constraint on $R$ from a neutrino oscillation experiment, excluding $R > 0.45~\mu$ m at 90 $\%$ C.L., as shown in Fig. 3. For $m_0 < 0.1~$ eV, LED mixing effects greater than about 6 $\%$ are excluded. Ongoing work includes the development of a new analysis framework that exploits the full power of both MINOS detectors and the analysis of MINOS+ beam data which significantly increases the number of events at higher neutrino energies, away from the three-flavor minimum where the model effects are bigger.

Figure 3: The 90 $\%$ C.L. data contour for the LED model, obtained using the Feldman-Cousins technique, based on $10.56\times10^{20}$ POT MINOS data and assuming normal mass ordering.

References

N. Arkani-Hamed, S. Dimopoulos, and G. R. Dvali, Phys. Lett. B. 429, 263 (1998).
I. Antoniadis, N. Arkani-Hamed, S. Dimopoulos, and G. R. Divali, Phys. Lett. B. 436, 257 (1998).
N. Arkani-Hamed, S. Dimopoulos, and G. R. Dvali, Phys. Rev. D. 59, 086004 (1999).
P. Minkowski, Phys. Lett. B. 67, 421 (1977).
M. Gell-Mann, P. Ramond, and R. Slansky, in Supergravity, p.315, edited by F. Nieuwenhuizen and D. Freedman, North Holland, Amsterdam, 1979.
T. Yanagida, Proceedings of the Workshop on Unified Theory and Baryon Number in the Universe, edited by O. Sawada and A. Sugamoto, KEK, Tsukuba, Japan, 1979.
R. N. Mohapatra and G. Senjanovic, Phys. Rev. Lett. 44, 912 (1980).
K. R. Dienes, E. Dudas, and T. Gherghetta, Nucl. Phys. B. 557, 25 (1999).
N. Arkani-Hamed, S. Dimopoulos, G. R. Dvali, and J. March-Russell, Phys. Rev. D. 65, 024032 (2001).
G. R. Dvali and A. Y. Smirnov, Nucl. Phys. B. 563, 63 (1999).
R. Barbieri, P. Creminelli, and A. Strumia, Nucl. Phys. B. 585, 28 (2000).
R. N. Mohapatra, S. Nandi, and A. Perez-Lorenzana, Phys. Lett. B. 466, 115 (1999).
R. N. Mohapatra and A. Perez-Lorenzana, Nucl. Phys. B. 576, 466 (2000).
R. N. Mohapatra and A. Perez-Lorenzana, Nucl. Phys. B. 593, 451 (2001).
H. Davoudiasl, P. Langacker, and M. Perelstein, Phys. Rev. D. 65, 105015 (2002).
P. A. N. Machado, H. Nunokawa, and R. Zukanovich Funchal, Phys. Rev. D. 84, 013003 (2011).
P. Adamson et al. (MINOS Collaboration), Phys. Rev. D. 94, 111101(R) (2016).

NO $\nu$ A

NOvA or NuMI Off-Axis $\nu_{\text{e}}$ Appearance is a two-detector long baseline neutrino oscillation experiment, similar in spirit to MINOS/MINOS+. Fig. 1 illustrates the basic design of the NO\nuA detectors. Through observation of the oscillation of muon neutrinos to electron neutrinos in the NuMI beam, NO $\nu$ A aims to measure $\theta_{13}$ and the CP violating phase $\delta_{\text{CP}}$ , and determine the neutrino mass ordering. In addition, through muon neutrino disappearance, NO $\nu$ A performs precision measurements of $\Delta m^2_{32}$ and $\theta_{23}$ . The NO $\nu$ A detectors consist of plastic PVC cells filled with liquid scintillator that are read out by WLS fibers coupled to avalanche photodiodes (APDs). A 330 metric-ton ND is located at Fermilab and a much larger 14 metric-kiloton FD in Ash River Minnesota, 810 $~$ km from the NuMI target. Unlike the MINOS detectors, the NO $\nu$ A detectors are located off-axis of the NuMI beamline such that they are exposed to a large neutrino flux corresponding to an energy of 2 $~$ GeV, the energy at which oscillations from muon neutrinos to electron neutrinos is expected to be at a maximum.

Figure 1: The basic design of the NO $\nu$ A detectors and readout system.

The UTKL Research Group has been involved in detector R $\&$ D, service work, and simulation efforts on NO $\nu$ A and is increasing its contributions to data analysis.

Learn more about Optical Simulations for NOvA performed by the UTKL Research Group below or visit the NOvA website.

NOvA Neutral Current Pion-Zero Production Measurement

This work aims to measure a cross section of neutrino induced neutral current $\pi^{0}$ production using the NOvA near detector. This type of interaction exchanges a $Z$ boson and is known as neutral current (NC). A neutrino undergoing a neutral current with at least one $\pi^{0}$ above threshold in the final state is the signal of the NC $\pi^{0}$ production analysis. $\pi^{0}$ decay into two gammas 99% of the time, so our signature for this analysis is two electromagnetic tracks slightly away from the vertex. NC $\pi^{0}$ production is a very important cross section when measuring electron neutrino appearance, since the two gammas or one of them can mistakenly be reconstructed as an electron. We start by simply selecting only events with 2 showerlike tracks (called prongs). We use a preselection of fiducial, containment and number of hits cuts to start. Several variables like the width, the gap and the invariant mass of the two prongs are fed to a Boosted Decision Tree, which also contains an electromagnetic shower identifier. The latter is obtained by training a convolutional neural network, which gets to learn how to identify electrons and photons from other particles. Below you find two event displays from the NOvA near detector and descriptions on how to make sense of all the pretty colors and labels.

The z-axis represents the beam direction and the two views within the same event display correspond to the top and side view of the detector. Only the small colored rectangles are the particle's energy deposits that translate into scintillation light within the NOvA cells. The amount of light collected is proportional to the energy deposited in each cell and the ADC scale at the bottom will help you map the different colors of the rectangles with different ADC counts. In particular, the redder the color, the higher the energy deposited and the bluer the smaller. In addition to the colored rectangles, you see the truth information for all particles in the event. All particles involved in each event have dotted lines associated with the direction of their trajectories. Both neutrinos are in blue and the true $\pi^{0}$ is in orange. The star highlights the true position of the vertex, whereas the cross stands for the reconstructed vertex. The lighter blue and pink dotted lines represent the direction of the two reconstructed tracks, which in this case coincide with the two gammas.

NOvA Neutron-Antineutron Oscillation

Searching for neutron anti-neutron oscillation is an active research direction that promises immense values for the field of particle physics and cosmology. Experimental observation of the phenomenon would offer the possibility of new physics associated with anomalous $B$ and $B-L$ violating processes. Understanding the mechanism of these processes is a key to explain the matter-antimatter asymmetry observed in our Universe.

Figure 1: Display of a $n+\bar{n}\rightarrow \pi^+ + \pi^- + 3\pi^0$ simulated event. This is example of one among 16 possible annihilation channels of antineutrons.

The signal and background simulations, the data-driven trigger and the offline analysis framework that allows the NOvA experiment to collect and analyze the signal-like events was developed by two former UTKL members. A 90\% C.L. sensitivity limit of $4\times10^{30}$ \,years is placed on the oscillation lifetime of bound neutrons inside the $^{12}$ C targets, assuming 7 years of exposure. This limit is equivalent to a sensitivity of $0.57\times10^{8}$ \,s placed on the oscillation lifetime of free neutrons.

Figure 2: Energy characteristic of signal events compared to that of background. This is one of 9 discrimination variables used in the offline analysis to separate signal events from the background.

NOvA Optical Simulation

Employing GEANT4, we simulated a benchtop setup, shown in Fig. 1, which measures the NO $\nu$ A cell light yield using both PMTs and APDs. The measured results are used to constrain the simulation where details on the photon generation and propagation inside the NO $\nu$ A cell are extracted.

Figure 1: A dark box was constructed as a housing for the setup. A plane of seven 1.1 $~$ m NO $\nu$ A cells was placed in the bottom container. This was filled with liquid scintillator to make sure the cells were fully immersed.

Figure 2: Number of photoelectrons dependencies on various hardware configurations from simulation. (a) Position of the fiber. The zero point and the maximum of the x-axis correspond to the cell center and PVC wall, respectively. (b) Scaling factor applied to the nominal PVC reflectivity. (c) Scintillator light yield. (d) Scaling factor applied to the nominal absorption length. (e) Fiber radius. (f) Fiber length.

DUNE

The Deep Underground Neutrino Experiment (DUNE) will consist of two underground detectors exposed to the world’s most intense neutrino beam. Equipped with a far detector that consists of four 10 metric-kiloton liquid argon time projection chambers and a near detector at a distance of 1300 km, this international collaboration aims to enter the precision era of neutrino oscillations. Its primary objectives are measurements of the mixing angles $\theta_{13}$ and $\theta_{23}$ , the charge-parity (CP) violating phase and determine the neutrino mass ordering. In addition, DUNE is sensitive to neutrinos from core-collapsed supernovae and will conduct proton decay searches.

Learn more about the DUNE PhotoDetection Simulation efforts going on in our group below or visit the DUNE website.

DUNE HaDeS

We are developing the Hadron Detection System(HaDeS) for DUNE. Ths is the system that'll help align the LBNF beamline. Where LBNF, thanks to PIP-2 is going to supply (I don't know this) of 120 GeV protons at the beamline. The protons will be steered towards a graphite target, to then decay into neutrinos and mesons. The mesons will than travel through the decay pipe where they'll decay into muons and neutrinos. HaDeS, will be placed at the end of the decay pipe measuring the mesons renmant, which are usually pions at the count and energy levels that DUNE will be operating at we'll need monitors to be able to measure the primary beam and tertiary charged particles to monitor beam quality, beam direction, and the operational integrity of the upstream beamline components. This work is crucial as if the beam is off center, than the uncertainty generated by that will skew and possibly make measurements at both the Near and Far detector worthless. Our work consists of both constructing and manually calibrating the physical monitor prototypes on site.

Figure 1: Placeholder for hopefully Nice chamber images, if not then discard this.

Figure 2: Placeholder for hopefully Nice chamber images, if not then discard this.

Our main focus is to create and test these prototype monitors. These monitors themelves consists of arrays of distinct ionization chambers. As we are only in the prototype stage, our arrays are 2x2 of ionization chambers. We are testing different sizes and calibration of the chambers in hope to find the most opitmal configuration for beam monitoring at DUNE.

DUNE PD Simulation

There are two possible geometries under consideration for the far detectors 10 metric-kiloton liquid argon TPCs. They are denoted with the names Single Phase, see Fig. 1, and Dual Phase geometry, see Fig. 2, which refer to the amount of matter states of the filling scintillator material, in this case: argon. The Single Phase geometry would only contain liquid argon and the Dual Phase would have mainly liquid argon but also some argon in gas form at the top of the detector.

Figure 1: A portion of DUNE’s Single Phase geometry TPC. APA = Anode Plane Assembly. CPA = Cathode Plane Assembly.

Figure 2: Dual Phase TPC design and working principle.

Our main focus is to work on computer simulations of optical photons in liquid argon, which will be of great importance for DUNE. Despite the immense physics potential of the DUNE experiment, the current state of simulations of optical photons propagating through liquid argon is not satisfying. Light detection is key to resolve time reconstruction and to apply crucial trigger conditions for proton decay and supernova neutrino searches. We study the light attenuation and volume scale issues that arise when going from the current relatively small liquid argon detectors to a 17 metric-kiloton chamber. Simulations are also used to determine the optimal light collection techniques (PMTs or SiPMs, optical fibers, or acrylic plates) and detector design.

Neutrino Oscillations